Публикации: Прочее (рубрикатор)

Мы с удовольствием публикуем работы конкурса «Моя лаборатория», который провели в рамках Олимпиады Программа «Мастерские инноваций» ФИОП РОСНАНО и МГУ имени М.В.Ломоносова.

В статье читатель познакомится с такими известными математическими задачами, как задача дискретной томографии и задача о максимальном потоке. Подробно изучив свойства этих задач, такие как существование и единственность решения, а также трудоемкость его нахождения, мы поймем, в чем заключается связь между ними, и рассмотрим алгоритмы их решения. Затем мы перейдем от теории к практике и обсудим, как сконструировать рабочую модель томографа и разработать программное обеспечение, которое будет основываться на рассмотренных математических задачах.

Введение

Статья обозревает проект «Дискретная томография», который был разработан в рамках областной летней естественнонаучной школы «Лаборатория-Z»[1].

По мнению автора, основной проблемой научно-исследовательских проектов по математике является отсутствие наглядности. Представьте себе школьную конференцию, на которой группа учеников-физиков демонстрирует собранную ими катапульту или радиопередатчик, группа химиков рассказывает про синтезированное ими мыло или духи, а группа математиков показывает доказательство новой теоремы из теории множеств. Результаты работ по естественнонаучным дисциплинам можно потрогать, увидеть, понюхать или даже попробовать запустить этим результатом снаряд, который улетит очень далеко. Как правило, математики довольствуются только слайдовой презентацией.

На самом деле эта абстрактная наука может оказаться наглядной и применимой в реальной жизни. Мы узнаем, как математики могут собрать рабочую модель томографа, который не стыдно будет показать на конференции рядом с катапультами, радиопередатчиками и духами. Наш прибор будет сканировать реальные объекты и воссоздавать их виртуальные копии. Причем, в отличие от 3-D сканера, томограф будет распознавать не только внешние очертания объекта, но и его внутренности.

Итак, томограф — это устройство, которое анализирует физический объект и на основе полученных данных создает его виртуальную модель. Наравне с 3-D принтерами они могут использоваться в создании прототипов изделий. Однако, сфер применения подобных устройств гораздо больше. Технологии томографии применяются в киноиндустрии, в медицине, в музейном деле, в промышленном дизайне и в индустрии развлечений, в строительстве и архитектуре. На разных этапах разработок и внедрения проектов томографы находят самое широкое применение. С помощью трехмерного сканирования можно оцифровывать культурное наследие, археологические объекты, предметы искусства. Широкое применение томографы нашли, прежде всего, в инженерии.

В нашем случае, разработка томографа состоит из трех частей: математика, инженерия и программирование. Задача математиков состоит в разработке принципов работы устройства. Самое главное для них – это ответить на вопрос, как по данным, собранным датчиками, восстановить структуру сканируемого объекта. Задача инженеров – это разработка конструкции прибора. От их решений зависит, насколько точны будут собранные данные об объекте. И, наконец, задача программистов заключается в объединении математики и инженерии. Они должны написать программный комплекс, который приводит в движение манипуляторы томографа, обрабатывает полученные датчиками данные, реализует математические алгоритмы вычисления, интерпретирует результат и затем строит 3-D модель. Теперь подробнее разберемся в каждой из составляющих проекта.

Математика

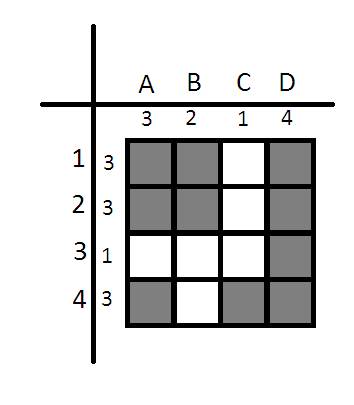
Обратимся к математической части будущего томографа. Для этого рассмотрим задачу дискретной томографии (сокращенно ЗДТ). Пусть задана таблица размера n*n, в которой некоторые клетки закрашены, а некоторые нет.

Причем известны: s1, s2, ..., sn - число закрашенных клеток в каждой из n строк. t1, t2, ..., tn - количество закрашенных клеток в каждом из n столбцов.

По этим данным требуется восстановить таблицу. Сначала займемся таким вопросом: всегда ли решение ЗДТ единственно?

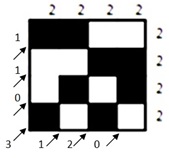
Рассмотрим пример таблицы 4*4, причем известно, что в каждой строке и в каждом столбце имеется ровно 2 закрашенные клетки. Иначе говоря s₁ = s₂ = s₃ = s₄ = 2, а также t₁ = t₂ = t₃ = t₄ = 2. И вот все варианты решения такой задачи с точностью до поворота:

Если бы томограф получил такие начальные данные, то обозреваемый объект мог бы с равной вероятностью выглядеть как один из 16ти вышеприведенных вариантов. Возникает проблема неоднозначности восстановления решения.

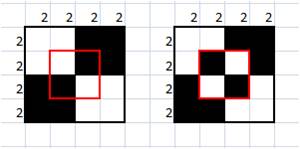
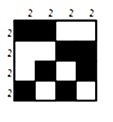
На самом деле, если более детально рассмотреть все варианты решения задачи, то можно разглядеть закономерность. Некоторые пары решений выглядят весьма похожими, имея лишь незначительные отличия:

И мы обнаруживаем квадрат размера 2*2, от поворота которого на 90 градусов, количество закрашенных клеток ни в строках, ни в столбцах не изменится. Такую таблицу 2*2 станем называть компонентой-переключателем.

Нетрудно догадаться, что задача для такой таблицы имеет ровно 2 варианта решения. Данный факт сомнению не подлежит. Такая маленькая задача с тривиальным решением будто бы встраивается в задачи большей размерности и порождает все новые варианты решения. Каждую такую компоненту в таблице можно “переключить”, то есть повернуть на 90 градусов, и получить новый результат.

Таким образом, мы разобрались, почему возникает неоднозначность решения, и далее, как часто говорят математики, скажем: “давайте рассматривать только те задачи, которые имеют ровно одно решение”. В дальнейшем мы будем работать только с таблицами без компонент-переключателей.

Очень скоро мы поймем, что ЗДТ можно решить достаточно просто и быстро. То есть, если мы запрограммируем описанный ниже алгоритм решения ЗДТ, то компьютер потратит мало времени для вычисления ответа. Конечно, скорость решения задачи компьютером зависит от объемов входных данных: чем больше размерность таблицы из ЗДТ, тем больше времени потребуется компьютеру для решения.

Однако существуют алгоритмы, для которых время вычисления увеличивается относительно медленно (по сравнению с другими алгоритмами) при росте объема входных данных. Самые яркие представители таких алгоритмов – это полиномиальные алгоритмы (напомним читателю что слово «полином» - это синоним слова «многочлен»). Они получили свое название из-за того, что время работы этих алгоритмов полиномиально зависит от объема входных данных. Грубо говоря, задачи, для которых существуют полиномиальные алгоритмы, решаются достаточно легко. А теперь рассмотрим модифицированный вариант ЗДТ: пусть известны не только количества закрашенных клеток по строкам и столбцам, но и по диагоналям.

Очевидно, что в такой постановке на конкретных входных данных мы получим гораздо меньше решений. Но за все приходится платить: оказывается [2], что для модифицированной ЗДТ не существует полиномиального алгоритма решения. Скорее всего, такую задачу можно решить только перебором всех возможных таблиц данной размерности. Такие задачи называют NP-трудными. Например, нам надо решить модифицированную ЗДТ для таблицы размером 4*4. Всего таких таблиц 2¹⁶ , значит, нам придется перебрать все эти варианты, что займет много времени. Конечно, компьютер сделает это за нас гораздо быстрее, но и для него будет трудным решить модифицированную ЗДТ, скажем, для таблицы 100*100.

Вернемся к нашей обычной ЗДТ. Теперь, когда мы уверены, что наша задача имеет единственное решение, приступим непосредственно к описанию алгоритма. Для решения ЗДТ мы будем использовать хорошо известную и изученную задачу о максимальном потоке (сокращенно ЗМП). Идея в следующем: мы превратим ЗДТ в ЗМП, затем решим новую задачу (для нее существует полиномиальный алгоритм!), после чего мы превратим решение ЗМП в решение ЗДТ. Чтобы сформулировать ЗМП, нам придется ввести несколько определений.

Граф — совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).

Граф называется взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Ориентированный граф G — это упорядоченная пара , где — непустое множество вершин или узлов, и — множество (упорядоченных) пар различных вершин, называемых дугами.

Транспортная сеть – это ориентированный ациклический (не содержащий циклов) взвешенный граф, где каждому ребру приписано неотрицательная пропускная способность, с двумя выделенными вершинами: источником и стоком, где любая другая вершина лежит на пути из источника в сток.

Поток — это функция, сопоставляющая каждой паре вершин число со следующими свойствами:

• поток между любыми двумя вершинами не может превысить пропускную способность их соединяющего ребра
• поток из вершины А в вершину В равен по модулю, но противоположен по направлению (имеет обратный знак) потоку из В в А
• для любой вершины сумма всех потоков, входящих в нее и исходящих из нее, равняется 0.

Задача о максимальном потоке заключается в нахождении такого потока в транспортной сети, что сумма потоков из источника в сток максимальна.

Итак, решение ЗДТ будет состоять из 3х этапов: построение по ЗДТ соответствующей ЗМП, решение ЗМП, по решению ЗМП восстановление решения ЗДТ.

Опишем процедуру построения ЗМП по входным данным ЗДТ. Итак, строим транспортную сеть, которая содержит вершины 4х типов: источник s, сток t, вершины-строки (первый столбец на рисунке слева), вершины-столбцы (второй столбец на рисунке слева).

Затем добавляем все дуги, соединяющие сток с вершинами-строками. Их пропускная способность равна количеству закрашенных клеток в соответствующей строке. Аналогично добавляем все дуги соединяющие вершины-столбцы со стоком и их пропускная способность равна количеству закрашенных клеток в соответствующем столбце.

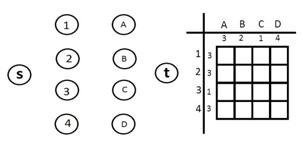
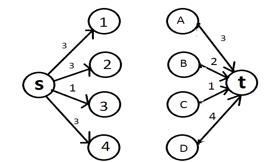
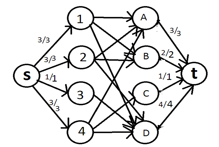Теперь добавляем все дуги, соединяющие вершины-строки с вершинами-столбцами с пропускной способностью 1. Эти дуги по сути символизируют клетки таблицы. Станем называть их дуги-клетки.

Построенную ЗМП можно эффективно решить, например, при помощи алгоритма Форда-Фалкерсона [3, 4]. И он всегда будет выдавать нам решение в силу того, что все параметры задачи – это целые числа. Этот алгоритм прекрасно описан в соответствующей литературе и мы не станем рассматривать его здесь.

По решению ЗМП решение ЗДТ восстанавливается следующим образом: мы закрашиваем те клетки, соответствуюшие вершины-дуги которых вошли в оптимальное решение ЗМП. Для нашего примера решение будет выглядеть, как показано на рисунке.

На этом, математическая часть проекта заканчивается. Мы разобрались, когда ЗДТ решается неоднозначно, а также научились решать ЗДТ через ЗМП при помощи алгоритма Форда-Фалкерсона.

Инженерия

Здесь мы рассмотрим конструкцию определенной модели томографа, который будет собирать для нас входные данные задачи дискретной томографии. Сразу скажем, что наша модель томографа будет скорее «игрушечной»: таким томографом нельзя будет просканировать тело человека. Более того, при такой реализации мы сможем работать только с вполне конкретными объектами и больше ни с чем. Однако, такую модель можно собрать самому в ближайшем центре робототехники вашего города. Напомним, что наша цель – это разобраться в том, как абстрактные и недоступные неподготовленному человеку математические теории переходят в реальную пользу, которую поймет любой. Также скажем, что наш вариант томографа не идеальный. Вы можете придумать свою реализацию, ведь инженерная задача – это очень творческий процесс. Но, в качестве примера, мы рассмотрим вариант, который был реализован в нашей лаборатории.

Итак, перейдем к рассуждениям: мы хотим создать механизм, который сканирует некий объект по разным направлениям и снимает некие показания, которые мы впоследствии переведем во входные данные ЗДТ. Понятно, что в такой постановке наше желание невозможно реализовать, потому что задача сформулирована очень неопределенно. Какие объекты мы будем сканировать? Каким образом мы будем это осуществлять? Что вообще подразумевает термин «сканировать»? Какие данные мы будем считывать прибором? Пока мы не ответим на эти вопросы, мы не сможем приступить к реализации томографа. Рассуждать над этими вопросами мы будем как настоящие математики – будем идеализировать и упрощать объекты, с которыми работаем, до тех пор, пока мы не сможем сформулировать строгую постановку задачи. Во-первых, договоримся, что мы будем сканировать только дискретные объекты. В самом деле, алгоритм решения ЗДТ подразумевает работу с таблицами, обозначающими дискретные фигуры - квадратики. В нашем случае идеализация следующая: мы будем рассматривать только фигуры, составленные из кубиков одного размера – это и есть наши дискретные объекты. Во-вторых, трехмерные фигуры мы будем сканировать по слоям, на каждый слой своя ЗДТ, в таблице которой закрашенная клетка обозначает наличие кубика в соответствующем месте слоя, а не закрашенная клетка – его отсутствие. В таком случае логично будет сконструировать томограф в виде рамки, которая перемещается по слоям фигуры и собирает входные данные ЗДТ на каждом «этаже». Разобравшись в том, как томограф работает на одном слое, можно легко распространить реализацию и на многослойную фигуру. После сбора данных на слое рамка перемещается на следующий слой и делает то же самое.

Теперь постановка нашей задачи выглядит более формально: есть трехмерная фигура, состоящая из кубиков одного размера. Требуется сделать томограф в виде рамки, которая сканирует фигуру по слоям. Каждый слой интерпретируется как таблица из ЗДТ. Далее нужно ответить на самый интересный вопрос – «как сканировать?». Будем честными, автор статьи сам долго ломал голову над этим вопросом. Напомним, что входные данные ЗДТ – это количества закрашенных клеток по строкам и по столбцам. Наш томограф необходимо обучить собирать некие данные, аналогичные входным данным ЗДТ. Основная трудность состоит в том, что томограф, в отличие от сканера, должен распознавать внутренность фигуры, а не только внешние очертания. То есть наш прибор должен воздействовать на фигуру не только снаружи, но и внутри, как бы проходить фигуру насквозь и собирать некие данные. Конечно, первое, что приходит в голову – это использовать рентгеновские лучи, но рентгеновский аппарат стоит дорого, и вряд ли вы найдете такой в центрах робототехники. Мы предлагаем более дешевый и простой вариант: вместо рентгеновских лучей использовать свет от лазера! Именно свет проходит объекты насквозь, правда, не через все объекты, но что мешает нам сделать кубики из подходящего материала? В нашей лаборатории мы пользовались полыми кубиками из затемненного оргстекла. Теперь представим себе такую картину: вы светите лазером на конкретное количество таких кубиков, выстроенных в ряд; за последним кубиком вы ставите ладонь и видите тусклую точку света от лазера; затем, вы убираете один из кубиков. При этом точка становится ярче, потому что луч света проходит через меньшее количество оргстекла, а значит, меньше рассеивается. Характеристика, отвечающая за яркость такой точки, называется освещенностью. Опытным путём можно убедиться, что по освещенности можно достаточно точно определить, через какое количество кубиков прошел лазер. Конечно, это утверждение выполняется при соблюдении некоторых условий: во-первых, замер освещенности должен проходить при одинаковом внешнем освещении; во-вторых, количество кубиков в ряду должно быть ограниченно небольшим числом – вряд ли вы найдете лазер с мощностью, позволяющей получить точку света при прохождении через 100 таких кубиков. В нашей лаборатории мы ограничились фигурами, попадающими в куб из 6х6х6 кубиков. При такой размерности лазер будет проходить не больше, чем через 6 кубиков. К тому же, расстояние между соседними кубиками будет не больше, чем в 4 кубика, что достаточно мало и позволит получать одинаковую освещенность точки вне зависимости от расстояния между кубиками в этих пределах.

Итак, данные, которые будет собирать наш томограф – это освещенность пучка света из лазера, проходящего сквозь ряд кубиков. Эта освещенность характеризует количество кубиков в соответствующей строке или столбце. Чтобы измерять нужную нам характеристику, мы использовали датчики освещенности из набора Lego Mindstorms NXT. Эти датчики передают освещенность в процентах от 0 до 100. При такой реализации нужно построить таблицу соответствия диапазонов освещенности и числа кубиков, через которые прошел лазер. Напомним, что все замеры должны проходить при одинаковой внешней освещенности, в помещении с другим светом вам придется строить другую таблицу соответствия. Если вы хотите демонстрировать работу вашего томографа в разных помещениях, вы, например, можете накрыть всю конструкцию (вместе со сканируемой фигурой) коробкой с отверстиями в местах, где будет светить лазер, и где будут стоять датчики. Такое решение позволит избежать воздействия внешнего света.

Теперь мы рассмотрим уже собранную нашей лабораторией конструкцию томографа для одного слоя. Чтобы прибор сканировал трехмерную фигуру, достаточно закрепить рамку на вертикальной оси и перемещать конструкцию от слоя к слою. Опустим технические детали сборки и программирования блоков NXT – всю необходимую информацию вы можете получить из инструкций по работе с наборами робототехники (в нашем случае – это Lego Mindstorms NXT и несколько деталей из TETRIX) и из инструкций по соответствующему программному обеспечению.

Наш томограф выглядит вот так:

Рассмотрим устройство по частям:

1. Рамка томографа, на которой жестко закреплены все остальные детали.
2. Мощный лазер, который посылает пучки света в датчики через кубики из оргстекла.
3. Зеркало, закрепленное на моторе. Его функция – направлять луч света так, чтобы он попадал в соответствующий датчик.
4. Зубчатые рельсы. По ним едет двигатель с зеркальцем, что обеспечивает переход луча от одного датчика к другому.
5. Датчики освещенности. При попадании света, датчик отправляет замеренную освещенность в блок NXT, а тот, в свою очередь, отправляет данные в компьютер. Также на датчиках закреплены светоуловители из фольги. После обработки одного слоя компьютер возвращает входные данные ЗДТ.
6. Блок NXT, в котором находится программа передачи данных на компьютер.
7. Второй блок NXT, оснащенный кнопкой, при нажатии на которую двигатель с зеркалом возвращается на начальную позицию.

На этом инженерная часть проекта завершается.

Программирование

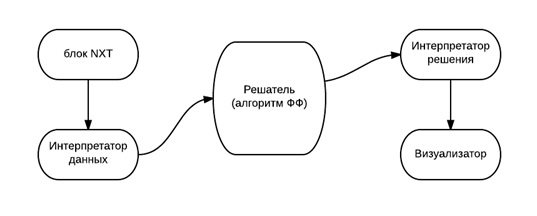
В этом разделе мы кратко опишем программный комплекс, который научит томограф собирать данные со слоя, преобразовывать их в ЗДТ, получать решение, а также создавать виртуальные объекты-копии. Конечно, мы не будем приводить здесь программный код, а ограничимся лишь общей блок-схемой реализации:

Каждый блок на этой схеме представляет собой отдельную программу. Опишем подробнее назначение каждой из них:

• Блок NXT собирает информацию с датчиков освещенности и передает ее интерпретатору данных.
• Интерпретатор данных, пользуюсь таблицей соответствий, составляет набор входных данных для ЗДТ.
• Решатель по входным данным ЗДТ строит соответствующую ЗМП, вычисляет ответ при помощи алгоритма Форда-Фалкерсона и передает его интерпретатору решения.
• Интерпретатор решения составляет набор входных данных для визуализатора.
• Визуализатор строит трехмерную модель объекта и выводит ее изображение на экран.

Все программы были написаны при помощи сред разработки PascalABC.NET, MonoDevelop, Unity Editor.

Заключение

Таким образом, в данной статье мы увидели, как при использовании математики, инженерии и программирования можно создавать действительно уникальные научные и промышленные проекты. Мы познакомились с задачей дискретной томографии и задачей о максимальном потоке, исследовали их свойства и научились находить решение. Также была рассмотрена конструкция сборки действующего томографа и план разработки программного обеспечения для нее.

Основной целью автора было продемонстрировать, что наука, в частности математика, это не только абстракции и сложные теоремы, но в первую очередь средство решения практических задач.

Ссылки и список литературы

[1] http://dio-gen.ru/lensh2014

[2] R.J. Gardner, P. Gritzmann, D. Prangenberg, On the computational complexity of reconstructing lattice sets from their X-rays. Discrete Math. 202 (1999), no. 1-3, 45-71.

[3] Ford, L. R.; Fulkerson, D. R. (1956). "Maximal flow through a network". Canadian Journal of Mathematics 8: 399. doi:10.4153/CJM-1956-045-5

[4] http://www.youtube.com/watch?v=yUFnDj4NH6c

Об авторе

Магистрант 2-го года обучения механико-математического факультета Новосибирского Государственного университета. C 2012 года преподает математику и робототехнику в Новосибирском Центре развития творчества детей и юношества «ДИО-ГЕН». Помимо подготовки школьников к олимпиадам, автор судит областные соревнования First Lego League по робототехнике и разрабатывает научно-исследовательские проекты для одаренных школьников.

.