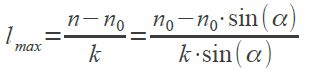Строгое решение:
При первом падении выполняется закон преломления sin(α)/sin(β)=n0.
Далее, ввиду неоднородности среды луч будет отклоняться от прямолинейного распространения так, как показано на рисунке. Если мысленно разбить волокно на множество тонких слоев, внутри которых показатель преломления можно считать постоянным, и воспользоваться законом преломления, то получим:
Касательная к траектории луча — это тангенс угла наклона к оси OX. Этот угол — есть угол преломления луча в точке с координатами (X, Y). Таким образом: 
Выполнив, ряд преобразований приходим к дифференциальному уравнению:
принимая во внимание начальные условия (при x=0, y=0), интегрируем почленно. Интеграл сводится к табличному. Дальнейшие выкладки позволяют найти расстояние, которое пройдет луч вдоль оси OX до противоположной грани (X1 ≈0,97 см). Это даёт возможность определить показатель преломления в этой точке n(X1) = 1,79 и угол полного внутреннего отражения на этом расстоянии βПВО = arcsin(0,56) ≈ 34°.
Рассчитав производную 
в точке с координатой X1, получаем угол падения луча к нижней гране ≈ 52°, что превышает угол полного внутреннего отражения. Таким образом, луч не выйдет из волокна.
Ввиду сложности строгого аналитического решения, допускалось приближенное, не учитывающее искривление траектории (приводится ниже). Участники предпринявшие попытку строгого аналитического решения получали максимальную оценку 5 баллов.
Приближенное решение:
Пренебрежем искривлением траектории луча внутри волокна, предполагая, что он распространяется прямолинейно. При первом падении выполняется закон преломления sin(α)/sin(β)=n0 (1 балл). Далее, луч внутри распространяется прямолинейно, падает и отражается под углом β, а вышедший луч преломляется под все большим углом, пока не будет выполнено условие полного внутреннего отражения 1/sin(β)=n(lmax) (1 балл).
Отсюда длина отрезка, от точки падения, до точки последнего выхода луча lmax,
определяется следующим образом:
,
Учитывая, что расстояние на поверхности от одного попадания луча до другого на противоположной стороне Δl=dtg(β), получаем число раз, которое луч выйдет из волокна 
(3 балла), то есть луч в этом приближении выйдет 1 раз на противоположной стороне.
