Новый родственник графена и изменение уравнение Шредингера для предсказания квазикристаллов — о свежих успехах российских ученых из МФТИ в исследовании новых материалов.
И не стекло, и не кристалл
Квазикристаллы отличаются от простых кристаллов тем, что в них нет бесконечной и всюду одинаковой кристаллической решетки. К примеру, кристалл поваренной соли можно разделить на одинаковые микроскопические кубики, но вот с квазикристаллами так поступить нельзя. Для того чтобы представить их атомную структуру, стоит взглянуть на изображение:
Пример квазикристалла (изображение: J.W. Evans, The Ames Laboratory, US Department of Energy)
Расположение атомов в квазикристалле непериодично. Примером бесконечной, но при этом непериодической структуры является мозаика Пенроуза, которая тоже непериодична и при этом составлена из абсолютно одинаковых элементов:
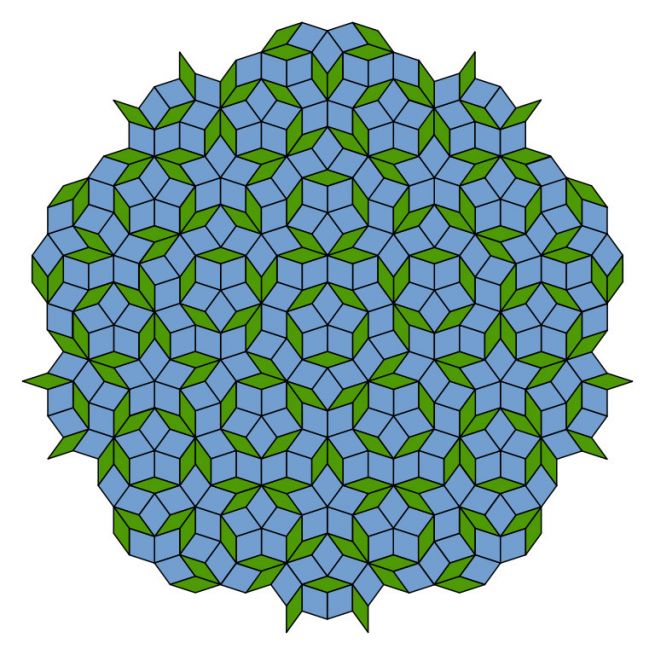Мозаика Пенроуза. Обратите внимание, что такая мозаика непериодична
Квазикристаллы были открыты только в 1982 году, хотя они встречаются и в некоторых природных минералах. Интерес ученых к квазикристаллам обусловлен не только их эффектной атомной структурой, но также рядом если не уникальных, то по крайней мере необычных свойств этих материалов.
Механически они занимают промежуточное положение между аморфными стеклами и кристаллами, а их электрическое сопротивление с понижением температуры увеличивается вместо того, чтобы уменьшаться.
Для того чтобы лучше понять возможности квазикристаллов, исследователям важно знать, как ведут себя внутри них электроны и электронную структуру квазикристалла. Электронная структура описывает распределение частиц внутри изучаемого объекта, и для ее расчетов необходимы квантовые методы: электроны ведут себя как квантовые объекты.
Поскольку электроны — квантовые частицы, то ученые говорят не просто о распределении частиц, положении точек в пространстве, а об электронной плотности. Для наглядности можно считать, что электроны размазаны вокруг атомов, а не сфокусированы в виде крошечных шариков.
Поведение квантовых объектов, как правило, описывается уравнением Шредингера.
Это уравнение было предложено Эрвином Шредингером еще в 1926 году, оно позволяет рассчитать динамику квантовой системы в заданном электрическом поле, но у него есть свои ограничения. В частности, любое изменение взаимного положения электронов приводит к изменению электрического поля, а уравнение этого не учитывает. Оно позволяет хорошо описать атом водорода с постоянным полем вокруг положительно заряженного протона, но даже для атомов побольше, с несколькими электронами, уравнение Шредингера просто так решить не получается.
Чтобы моделировать сложные системы из многих электронов, учеными предложено множество методов. Все они так или иначе упрощают конфигурацию электрического поля — например, игнорируя часть электронов в атоме или пренебрегая сдвигами ядер атомов в кристаллической решетке. Если считать, что кристаллическая решетка всюду одинаковая, то расчеты электронной структуры кристалла можно сразу упростить рассмотрением периодического поля. С квазикристаллом такой прием не срабатывает.
Метод, описанный Игорем Блиновым в журнале Scientific Reports, позволяет обойтись без длительных и потому дорогих численных расчетов.
Физик предложил модифицировать уравнение Шредингера таким образом, что на его решение можно накладывать периодические начальные условия — проще говоря, рассматривать квазикристалл как многомерную структуру, соответствующую «нормальному» кристаллу.
Ученый обратился к тому факту, что квазипериодическая функция, описывающая распределение зарядов в пространстве, может быть при помощи определенного математического приема преобразована в периодическую, но большей размерности (от большего числа переменных). Игорь Блинов приводит в своей статье следующий пример: квазипериодическая одномерная функция f(x) = sin(x) + cos(√(2x)) может быть преобразована в периодическую, если ввести дополнительную переменную y = √(2x).
Иллюстрация из статьи Игоря Блинова. Превращение апериодической функции в периодическую за счет ввода дополнительной переменной
Аналогичный прием, если его использовать к функции, описывающей распределение электронов в квазикристалле, позволяет получить периодическую картину и упростить уравнение Шредингера, сделав намного удобнее расчеты электронной конфигурации перспективных материалов.
Сам Игорь Блинов комментирует свой результат следующим образом: «Работа, опубликованная в Sci. Rep., делает процедуру нахождения электронной конфигурации в квазикристаллах более наглядной и более точной, чем некоторые из уже существующих методов ее определения, такие как метод кристаллических апроксимантов. Описанный метод, вероятно, поможет в будущем предсказывать структуру и свойства квазипериодических материалов — то, что для кристаллов умеет и успешно делает лаборатория компьютерного дизайна в МФТИ под руководством Артема Оганова».
Родственник графена
Собственно, сам Артем Оганов и возглавляемая им группа ученых из России, США и Китая с помощью компьютерного моделирования предсказала существование нового углеродного двумерного материала — «лоскутного» аналога графена, который они назвали фаграфеном. Результаты исследования опубликованы в журнале Nano Letters.
«В отличие от графена, который образован шестиугольными сотами с атомами углерода в узлах, фаграфен состоит из пяти-, шести- и семиугольных углеродных колец. Отсюда и его название — сокращение от Penta-Hexa-heptA-graphene», — пояснил Артем Оганов, руководитель лаборатории компьютерного дизайна материалов МФТИ.
Двумерные материалы — материалы, состоящие из слоя толщиной в один атом, — в последние десятилетия привлекают большое внимание ученых. Впервые такой материал — графен — был получен в 2004 году Андреем Геймом и Константином Новоселовым, за что в 2010 году они получили Нобелевскую премию по физике.
Благодаря своей двумерности графен имеет абсолютно уникальные свойства.
Обычные материалы способны проводить ток в том случае, если свободные электроны могут иметь энергию, соответствующую зоне проводимости данного материала. Если между диапазоном возможных энергий электронов («валентная зона») и диапазоном проводимости есть разрыв (так называемая запрещенная зона), то этот материал — изолятор. Если «валентная зона» и «зона проводимости» перекрываются, то это проводник — материал, где электроны могут перемещаться под действием электрического поля.
В графене каждый атом углерода имеет три электрона, которые связаны с электронами атомов-соседей, образуя химические связи. Четвертый электрон каждого атома делокализован по всему графеновому листу, что позволяет ему проводить электрический ток. При этом в графене запрещенная зона имеет нулевую ширину. Если представить энергию электронов и их положение в виде графика (как на этой картинке к статье), получится фигура, похожая на песочные часы, — два конуса, соединенных вершинами, — так называемые конусы Дирака.
Благодаря этому электроны в графене ведут себя очень странным образом: они все имеют одну и ту же скорость, которая оказывается сопоставимой со скоростью света, и не обладают инерцией.
Это выглядит так, как будто они не имеют массы. Примерно так же, согласно теории относительности, должны вести себя частицы, путешествующие со скоростью света.
Скорость электронов в графене составляет около 10 тыс. км/с (в обычном проводнике скорость электронов — от сантиметров до сотен метров в секунду).
Фаграфен, открытый Огановым и его коллегами с помощью алгоритма USPEX , как и графен, является материалом, где возникают «конусы Дирака», а электроны ведут себя как безмассовые частицы.
«При этом в фаграфене из-за разного числа атомов в кольцах «конусы Дирака наклонены, поэтому скорость электронов в нем зависит от направления. В графене это не так. Это может быть очень интересно для будущих практических применений, где полезно варьировать скорость движения электронов», — говорит Оганов.
Фаграфен имеет все другие свойства графена, которые позволяют рассматривать его как перспективный материал для гибких электронных устройств, транзисторов, солнечных батарей, дисплеев и многого другого.
