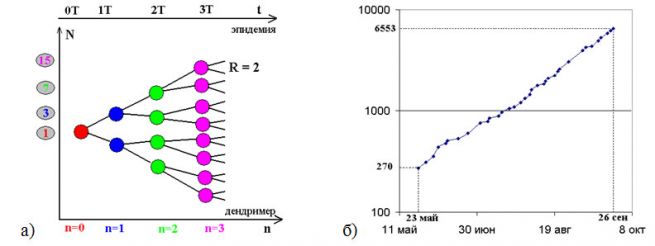
Рис. 1.
а) Схематичное представление классической модели неограниченного роста для R = 2.
б) Рост суммарного числа заболевших* от вируса Эбола в Гвинее, Либерии и Сьерра-Леоне за 126 дней (на основе данных ВОЗ).
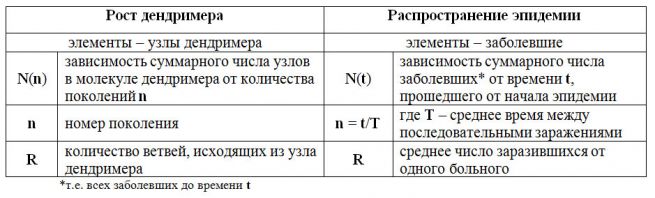
Классическая модель неограниченного роста (рис. 1а) может быть использована для описания процессов роста разветвленной молекулы дендримера, роста популяции бактерий или распространения эпидемии. Основной параметр этой модели – коэффициент R, который показывает, во сколько раз число элементов в текущем поколении больше числа элементов в предыдущем поколении.
1. Выведите формулы N(n) и, соответственно, N(t). (3 балла)
2. В каких координатах и при каком условии зависимость N от времени t линеаризуется? Чему будет примерно равен тангенс угла наклона полученной прямой? Поясните. (3 балла)
3. В случае эпидемии оценка коэффициента R позволяет делать прогнозы и определять эффективность принимаемых мер. Если удается снизить R < 1, то эпидемия идет на спад. На основании данных рис. 1б найдите R за рассмотренный промежуток времени, считая, что полученную зависимость N(t) можно использовать для описания непрерывного процесса эпидемии и T = 10,9 дня. (3,5 балла)
4. Считая R и T постоянными во времени, найдите дату начала эпидемии, а также к какой дате (если бы не были приняты меры по снижению R) суммарное количество больных могло бы достичь 1 000 000 человек. (3,5 балла)

