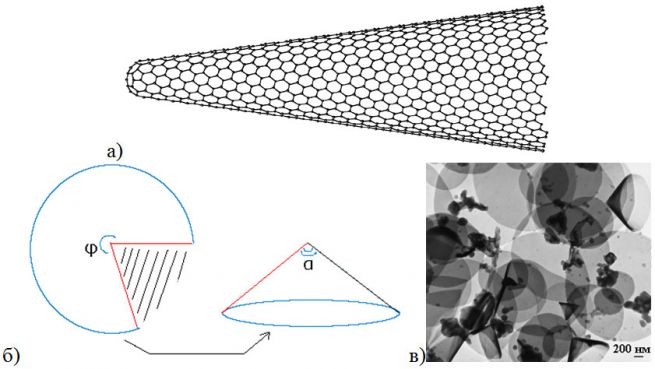
Рис.1 а) Модель углеродного наноконуса; б) развертка конуса и сам конус, здесь φ – угол развертки, α – угол раствора*; в) ПЭМ изображение углеродных кругов и наноконусов.
Если из плоского листа вырезать сектор, а затем склеить этот лист по линии разреза (рис. 1б) – получится конус.
1. Выведите выражение, связывающее угол развертки конуса φ с углом раствора конуса α. (1,5 балла)
Если в условиях роста круглых графеновых листов углеродный зародыш содержал дефекты, то может получиться углеродный наноконус (УНК) (рис. 1в). Чтобы получить из графенового листа конус, необходимо «вырезать» из него сектор (сектора) так, чтобы образовавшиеся края можно было склеить по углеродным связям. При этом при вершине конуса образуется содержащая дефекты «шапочка», которая и задает угол раствора α остальной части листа графена (рис. 1а). В дальнейшем будем считать, что УНК состоит только из шести- и пятиугольников (последние - как дефекты в «шапочке»).
2. Сектор с каким углом необходимо удалить из графеновой сетки, чтобы образовался пятиугольник?(1 балл) Сколько пятиугольников может содержать «шапочка» при вершине конуса? (2,5 балла)
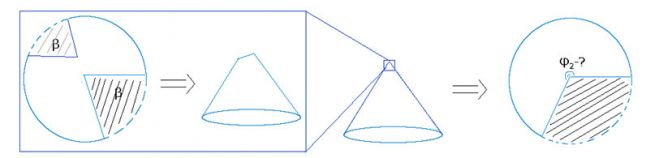
Рис. 2. Удаление второго сектора в конусе.
3. Поясните, как рассчитать эффективный угол развертки φ2 (рис. 2), если на небольшом (по сравнению с размерами конуса) расстоянии от его вершины удалить дополнительный сектор с углом β, равным углу ранее удаленного сектора. (1,5 балла)
4. Рассчитайте все возможные углы раствора α углеродных наноконусов. (2,5 балла)
5. Можно ли по ПЭМ-изображениям (рис. 3) однозначно определить, сколько пятиугольников содержится в «шапочке» каждого углеродного наноконуса? Поясните ход решения и свой выбор. (6 баллов)
Подсказка. На ПЭМ изображениях УНК выглядят полупрозрачными, однако угол, под которым видны конусы, неизвестен. Для ответа на вопрос нет необходимости проводить сложные расчеты, можно просто творчески подойти к решению.

Рис. 3. Различные ПЭМ изображения наноконусов.
*Угол раствора конуса α - угол между двумя противоположными образующими (угол при вершине конуса).
Вспомогательный материал к задачам по математике: сетка шестиугольников.

