Согласно правилу Хюккеля, двухмерные (плоские) молекулы, содержащие общую электронную систему из 2(2N+1) π-электронов, обладают особыми физико-химическими свойствами и являются ароматическими, например, молекула бензола, содержащая 6 π-электронов (N = 1).

Интересно, что похожее правило существует и для трехмерного случая, если обобществляемые электроны считать сферическим электронным газом, окружающим «сферический» атомный кластер в вакууме. Квантово-механический расчет для такой системы приводит к молекулярным орбиталям, которые описываются всего двумя квантовыми числами – орбитальным квантовым числом l (0, 1, …, N) и магнитным квантовым числом m (-l,…, 0, …, +l). Образовавшиеся молекулярные орбитали формой и вырожденностью напоминают обычные атомные (s, p, d, f, …) орбитали, поэтому электронные оболочки кластера похожи на подуровни атомов. Аналогично атомам и ионам с электронными конфигурациями инертных газов, «сферические» кластеры, имеющие полностью заполненные молекулярные орбитали, могут обладать особыми физико-химическими свойствами (ароматичностью) и, подобно ароматическим органическим соединениям, повышенной стабильностью.

1. Какое максимальное число электронов содержится в 0, 1, 2, 3, 4, … N-й оболочке такого кластера? Сколько суммарно электронов будет у кластера со всеми полностью заполненными оболочками вплоть до 0, 1, 2, 3, 4, …, N-й? Найдя формулу зависимости суммарного числа электронов от N, вы получите трехмерный аналог правила Хюккеля. (2,5 балла)

2. Считая, что π-электроны фуллеренов будут заполнять приведенные выше молекулярные орбитали, рассчитайте, какие фуллерены с количеством атомов до 100 могли бы обладать ароматичностью. (2 балла)

3. Какие минимальные заряды должны приобрести фуллерены C₂₀ и C₆₀ для образования ароматических ионов? (1 балл)

Применение концепции ароматичности находит широкое практическое применение при решении задач, связанных с геометрией различных кластеров и молекул.

Как правило, среди изомеров фуллеренов наиболее стабильными оказываются те, у которых имеется наименьшее количество пятиугольников с общими ребрами, поскольку они обладают меньшим напряжением (например, всем известный бакибол C₆₀ – самый маленький фуллерен с изолированными пятиугольниками). Однако, среди приведенных на рисунке двух изомеров А и Б некоторого фуллерена, более стабильным является не изомер А, имеющий большее число изолированных пятиугольников, а изомер Б, характеризующийся меньшим диаметром описанной окружности.

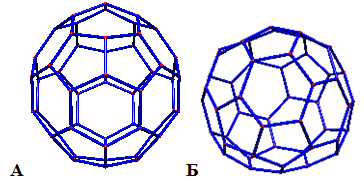
4. Какова формула этого фуллерена? (0,5 балла) Почему изомер Б более стабилен? (2 балла)

5. Какое расположение атомов цезия вокруг атома кальция в кластере Cs₅Ca⁺ будет предпочтительным: в виде плоского пятиугольника, или в виде тригональной бипирамиды? Ответ поясните. (2 балла)