В 1887 году Уильям Томсон (лорд Кельвин) задался вопросом: как разбить трехмерное пространство на одинаковые по объему многогранники так, чтобы площадь их стенок была минимальна (задача одинаковых пузырьков в пене). С тех пор данная проблема носит название задачи Кельвина.
В 1993 году в качестве решения задачи Кельвина была предложена структура Уэйра-Фелана. В ее основе – заполнение пространства 12-ти и 14-тигранниками (рис. 1). В этой структуре 14-тигранники связаны друг с другом через шестиугольные грани в цепочки, которые, в свою очередь, выстраиваются в трех взаимно перпендикулярных направлениях, образуя трехмерный каркас с 12-тигранными пустотами между ними.
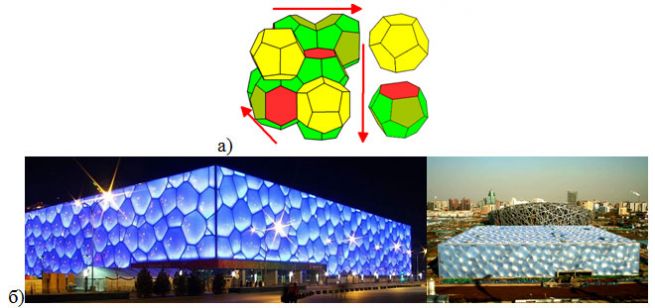
Рис. 1. а) Структура Уэйра-Фелана и составляющие ее многогранники. б) Пекинский национальный плавательный комплекс, построенный к Олимпиаде 2008 года в Пекине на основе этой структуры. Такой подход к дизайну позволил получить более легкую и прочную конструкцию.
Похожее на структуру Уэйра-Фелана решение используется природой при построении простейших газовых гидратов – соединений включения, в которых молекулы гостя находятся в клетках-«нанопузырьках», образованных молекулами воды (рис. 2.).
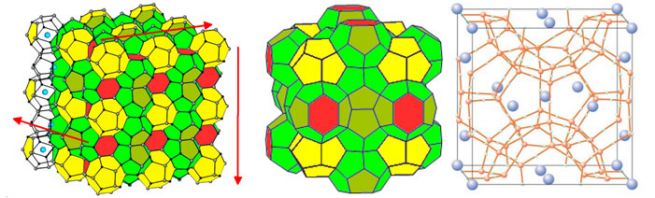
Рис. 2. Структура простейшего клатрата - газогидрата, отвечающая структуре Уэйра-Фелана. Построена из двух правильных многогранников: додекаэдра (12 граней, 20 вершин) и тетрадекаэдра (14 граней, 24 вершины). Молекулы гостя занимают центры всех ячеек.
1. Какие еще материалы можно назвать нанопеной? (1 балл)
2. Структура какого наноматериала является решением двумерного случая задачи Кельвина (разбиение плоскости на равные ячейки с минимальным периметром)? (1 балл)
3. Соответствует ли структура простейшего клатратного каркаса условиям задачи Кельвина? Ответ поясните. (2.5 балла)
4. Какие связи связывают структурные единицы простейшего клатрата в каркас? Какова при этом валентность и гибридизация узлового атома? (1 балл)
5. Атомы и соединения атомов какой группы Периодической таблицы должны быть склонны к образованию такого типа клатратов, почему? Приведите несколько примеров. (2 балла)
6. Где могут найти применение клатраты с такой структурой? Приведите три примера. (2.5 балла)