Напомним, что фуллерены — это молекулы Cn, причём атомы являются вершинами многогранника, все грани которого — пятиугольники и шестиугольники. Подробнее об устройстве фуллеренов можно узнать, решив задачу «Низшие фуллерены», или поискав информацию в сети Интернет.
В таблице представлены результаты вычислений суммарной энергии атомов фуллеренов с разным количеством атомов. Три правых колонки таблицы — полудиаметры молекулы фуллерена, измеренные в трех разных направлениях.
- (а, 1 балл) Авторы статьи предлагают считать «истинную» энергию, приходящуюся на один атом фуллерена, по формуле
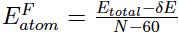(вместо естественной формулы 
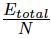), чтобы исключить вклад пятиугольников. Здесь δE — суммарная энергия атомов фуллерена C60. Вычислите «истинную» энергию, приходящуюся на один атом, в каждом фуллерене из этой таблицы. - (б, 3 балла) Какая зависимость лучше всего описывает поведение EFatom при росте радиуса фуллерена:
EFatom = E0 + Cr-1, EFatom = E0 + Cr-2, EFatom = E0 + Cr-3 (для некоторых значений E0 и C)? Здесь r — радиус сферы, приближающей фуллерен. - (в, 2 балла) Как найденное значение E0 соотносится с энергией, приходящейся на один атом в плоском листе графена? Попробуйте объяснить полученное соотношение.
|
атомов (N) |
Etotal (эВ) |
a-axis (Å) |
b-axis (Å) |
c-axis (Å) |
|
60 |
−531.33 |
3.335 |
3.419 |
3.475 |
|
70 |
−622.58 |
3.465 |
3.542 |
3.973 |
|
76 |
−676.39 |
3.357 |
3.831 |
4.381 |
|
78 |
−693.86 |
3.576 |
3.679 |
4.298 |
|
80 |
−711.77 |
3.864 |
3.929 |
4.056 |
|
84 |
−748.46 |
3.277 |
4.250 |
4.791 |
|
100 |
−894.22 |
3.881 |
4.052 |
5.635 |
|
180 |
−1629.66 |
5.999 |
6.085 |
6.194 |
|
240 |
−2181.51 |
6.958 |
6.941 |
7.241 |
|
320 |
−2913.64 |
7.928 |
8.165 |
8.521 |
|
500 |
−4569.75 |
9.902 |
10.247 |
10.853 |
|
540 |
−4940.30 |
10.505 |
11.364 |
11.894 |
