История вопроса началась в 1867 году, когда великий английский физик Дж. Максвелл предложил мысленный эксперимент для доказательства статистической природы Второго закона термодинамики. Слово «демон» для обозначения гипотетического устройства, разделяющего молекулы на «горячие» и «холодные», появилось несколько лет спустя. Долгое время считалось, что экспериментальная реализация мысленного эксперимента Максвелла позволит опровергнуть Второй закон, однако после долгих дискуссий физики, математики и химики пришли к единому мнению, что работа «демона» не нарушает Второй закон. Она сводится к превращению информации в энергию, причем закон сохранения энергии не нарушается – просто энергия под действием информации переходит из одной части системы в другую или черпается из окружающей среды.
Авторы настоящей работы предложили такую версию «демона». Представим себе микроскопическую частицу, находящуюся на спиральной лестнице, причем высота ступенек сравнима с энергией теплового движения kT, так что частица может за счет собственной энергии забраться на более высокую ступеньку, а может опуститься ниже (рис. 1.а). В среднем, вторые переходы происходят чаще, чем первые, поэтому за большой промежуток времени частица самопроизвольно опустится вниз на какое-то число ступенек.
Теперь включим в систему «демона», который наблюдает за перемещениями частицы и сразу после того, как она прыгнет на верхнюю ступеньку, поставит заслонку, блокирующую движение вниз, так что теперь частица может двигаться только в одном направлении – вверх. После следующего скачка ставится новая заслонка и т.д. В результате частица поднимается вверх по лестнице и ее потенциальная энергия все время растет. За счет чего это происходит? Первая мысль – за счет энергии, вносимой в систему при постановке заслонки. Однако, это не так – авторы утверждают, что эта энергия может быть сделана бесконечно малой (это – единственное спорное (очень спорное) утверждение в данной статье). На самом деле, энергия берется из окружающей среды под влиянием информации, получаемой при измерении положения частицы – то есть, информация превращается в энергию. Получается, что в основе неравномерного распределения энергии – управление с обратной связью.
Идея – достаточно простая и не оригинальная, аналогичное устройство было предложено еще в 1929 году американским физиком венгерского происхождения Лео Сциллардом. Но техническая реализация этой идеи потребовала большого экспериментального искусства. Вот как это было сделано. В стеклянную кювету размером несколько десятков микрон, заполненную буферным раствором, поместили частицу, состоящую из двух полистирольных шариков диаметром 287 нм, один из которых прикреплен с помощью молекулы-линкера к поверхности стекла, а другой может совершать вращательное броуновское движение (рис. 2.а). К противоположной поверхности подключили электроды, создающие переменное электрическое поле. Это поле вызывало поляризацию диэлектрика, из которого была изготовлена частица, и создавало для нее периодический потенциал с небольшим наклоном, который обеспечивал предпочтительное вращение в одну сторону (рис. 2.b). За движением частицы следили с помощью микроскопа, а сигнал записывали на высокоскоростную видеокамеру и передавали в компьютер. Как только оказывалось, что частица повернулась в «невыгодную» сторону, против поля, компьютер включал обратную связь и поле переключалось (рис. 2.с, правый столбец) – «демон» включался в работу. Если поле переключалось достаточно быстро, пока частица не вернулась обратно, ее новое положение фиксировалось и энергия частицы увеличивалась, причем рост превышал затраты на переключение поля.
На рис. 3 показана траектория частицы под управлением «демона» – она напоминает движение вверх по потенциальной лестнице – тем самым мысленный эксперимент, описанный в самом начале, реализован с помощью коллоидной частицы в переменном электрическом поле с обратной связью.
В энергию в данном случае превратилась информация об угле поворота частицы. В идеальном случае, при полном переходе информации в энергию один бит превращается в энергию kT ln2. В эксперименте, описанном в статье, эффективность такого перехода оценивается в 28%. Но здесь важно не число, а сам факт, прецедент. Очень важно еще раз подчеркнуть, что энергия не взялась со стороны, она уже находилась в системе, информация просто помогла создать поток этой энергии внутри системы, который, на первый взгляд, противоречит Второму закону.
Что же будет дальше? Перспективы данной работы связаны с дальнейшим углублением в нано-область. Авторы предлагают использовать свой метод для передачи энергии наноустройствам, например наномоторам и надеются в будущем создать «демона Максвелла» не макро-, как в данной работе, а нано-размеров.
Но на мой взгляд, данная работа важна не приложениями, а демонстрацией фундаментальных принципов: 1) принципа перехода информации в энергию в результате обратной связи и 2) Второго закона термодинамики. Авторы еще раз экспериментально подтверждают, что для объединенной системы «частица в растворе + «демон» Второй закон не нарушается.
И все-таки, его можно нарушить! Правда, только для малых систем и в течение очень короткого времени – за счет флуктуаций. В 1993 году австралийские ученые доказали флуктуационную теорему, в которой аналитически найдена вероятность того, что диссипативный поток в фазовом пространстве движется в направлении, нарушающем Второй закон. Если на некоторой фазовой траектории за время t производится энтропия равная A (в относительных единицах), а на другой траектории энтропия уменьшается на эту же величину, то отношение вероятностей этих двух траекторий экспоненциально растет с ростом A: [Формула 1]
Поскольку энтропия – экстенсивная величина, она растет пропорционально числу частиц. Таким образом, для макроскопических систем энтропия A велика, и доля фазовых траекторий, на которых нарушается Второй закон, ничтожна – практически равна 0.
Эта теорема была проверена с помощью молекулярно-динамичеких расчетов и подтверждена в эксперименте (G. M. Wang et al., Phys.Rev. Lett. 89, 050601 (2002)), где изучались траектории броуновского движения коллоидной частицы микронных размеров, находящейся в оптической ловушке. Число траекторий, подтверждающих и нарушающих Второй закон, количественно соответствовало флуктуационной теореме. Интересно другое: совершенно неожиданно выяснилось, что траектории, нарушающие Второй закон, могут наблюдаться в течение очень долгого (для флуктуаций) времени – вплоть до нескольких секунд. Разумеется, при t, стремящемся к бесконечности, «неправильные» траектории исчезают, в полном соответствии со Вторым законом. Так что законы природы выдержали еще одну экспериментальную проверку и как всегда устояли!
По материалам статьи Toyabe S., Sagawa T., Ueda M., Muneyuki E., Sano M. "Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality", Nature Physics doi:10.1038/NPHYS1821 (2010).
Профессор В.В.Еремин, химический факультет МГУ
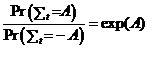
). Теперь об эксперименте. Выполненная конструкция представляет собой своеобразный "генератор механических колебаний" 
. Внешнее поле в этом эксперименте за счет обратной связи будет переключаться с некоторой средней частотой, зависящей от температуры окружающей среды, и вызывать усиление движения. В итоге из-за возникающей корреляции в системе "частица-поле" случайное броуновское движение постепенно превратится в упорядоченное колебание частицы с большей энергией. Энергия колебаний частицы, очевидно, не будет превышать энергию внешнего возбуждения. 
. 
