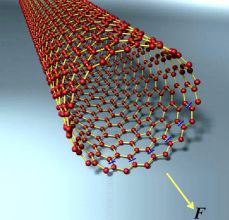
Возьмём одностенную нанотрубку типа «зиг-заг» (см. рис. 1). Закрепим невидимый конец трубки, а к другому её концу приложим растягивающую силу F.
Пусть в нанотрубке атомы углерода образуют между собой одинаковые связи (С-С, сигма-связи), а углы между ними равны 120о. Тогда при растяжении нанотрубки эти связи будут растягиваться одинаково. Однако разорваться нанотрубка может самым причудливым образом, зависящим, например, от того, какая С-С связь разорвётся первой.
Чтобы упростить расчёты, предположим, что растяжение разрывает только С-С связи, ориентированные вдоль оси трубки и расположенные в одной плоскости её поперечного сечения (линии разрыва обозначены синим на рис. 1).
Известно, что расстояние d между ближайшими атомами углерода в нанотрубке приблизительно равно d=0,15 нм. Легко показать, что если диаметр трубки равен D, то количество N связей, ориентированных вдоль оси трубки равно:
N = pi*D/(d*1,73) (1)
При этом к каждой С-С связи приложена сила, равная F/N.
Чему равна прочность одной С-С связи?
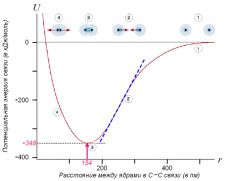
Найти прочность С-С связи можно из графика зависимости потенциальной энергии U этой связи от расстояния между атомами (рис. 2).
Из графика на рис.2 следует, что потенциальная энергия связи достигает минимума, когда расстояние между ядрами атомов составляет 154 пм. Это и определяет расстояние, на котором находятся атомы углерода в нерастянутой нанотрубке.
Тангенс наклона касательной правой ветви кривой на рис.2 пропорционален силе F1, необходимой для того, чтобы растянуть и удерживать атомы на данном расстоянии r :
F1 = (dU/dr)/NA ,
где NA – число Авогадро, 6.1023 моль-1.
Чтобы увеличить расстояние между атомами углерода, надо приложить силу F1, и если эта сила будет больше максимального тангенса угла наклона (см. синий пунктир на рис. 2), то С-С связь порвётся. Простые расчёты (вычисление см. ЗДЕСЬ) показывают, что эта связь порвётся при
F1 > 3,8 нН.
Чему равна прочность одностенной нанотрубки?
Нанотрубка разорвётся, когда сила F, растягивающая трубку, станет больше 3,8.N нН, где N - число параллельных оси C-C связей в одном поперечном сечении трубки. Пусть диаметр нанотрубки D = 1,5 нм. Тогда из формулы (1) следует, что N = 18. Поэтому нанотрубка разорвётся при Fmax = 69 нН.
Чтобы вычислить прочность Пmax нанотрубки, разделим Fmax на площадь поперечного сечения S = pi*D2/4 и получим:
Пmax = 39 ГПа.
Значение прочности нанотрубки, полученное нами теоретически, довольно близко к максимальным экспериментально полученным величинам (63 ГПа) и, как и следовало ожидать, гораздо больше прочности самых прочных сортов стали (0,8 ГПа).
Как посоветовал Чеширский В.В. (см. ниже в комментариях), чтобы окончательно свести теоретические "концы" с экспериментальными, достаточно для межатомной связи использовать параметры ароматической (упрощенно полуторной) связи с энергией 509 кДж/моль. Далее, возможно несколько упрощенно, предполагая пропорциональное увеличение наклона касательной на графике потенциальной энергии, получим, что прочность такой "реальной" нанотрубки станет равной 57 ГПа. Так теория становится ближе к практике!
Отметим, что у многостенных нанотрубок прочность будет в несколько раз выше!
Информацию о других "загадочных" явлениях наномира можно найти в научно-популярной лекции «Что могут нанотехнологии», а ссылки на другие публикации - на личной страничке автора.