Публикации: Оптика и электроника (рубрикатор)

В наномире изменяются не только механические свойства, температуры плавления веществ, но и их электрические характеристики. В статье, опубликованной в 1998 году в журнале Science (Frank с сотр., Science, т. 280, с. 1744), показано, что сопротивление R цилиндрического резистора наноразмеров нельзя вычислять по известной формуле

R=ρL/S ,

где L – длина, S – площадь поперечного сечения, а ρ - удельное сопротивление материала резистора. Оказалось, что сопротивление R₀ нанорезисторов вообще не зависит от их размеров и вещества, из которого они сделаны, а определяется только двумя фундаментальными физическими константами

R₀ =h/(2e²)=12,9 кОм, (1)

где e – заряд электрона (1,6×10^-19 Кл), а h – постоянная Планка (6,6×10^-34 Дж^.с). Величину R₀ назвали квантом электрического сопротивления, имея ввиду, что в наномире сопротивления всех резисторов одинаковы.

Квантование электрического сопротивления – не единственная особенность проводимости в наномире. Оказалось, что в нанорезисторе не выделяется «джоулево тепло» при прохождении тока. Эту необычную проводимость в наномире, независящую от длины резистора, площади его поперечного сечения и не сопровождающуюся выделением теплоты, назвали баллистической (от греч. ballo – бросаю; баллистика - наука о движении артиллерийских снарядов, пуль и т.п.). Этим названием его авторы хотели подчеркнуть, что электроны, как искусно запущенные снаряды, движутся через нанорезистор, не сталкиваясь с его атомами, находящимися в узлах кристаллической решётки.

Углеродные нанотрубки – квантовые резисторы

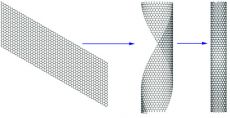
Примером нанорезисторов, обладающих баллистической проводимостью, являются углеродные нанотрубки - протяженные цилиндрические структуры диаметром от одного до нескольких десятков нанометров и длиной до нескольких сантиметров. Нанотрубки – это каркасные структуры или гигантские молекулы, состоящие только из атомов углерода. Углеродную нанотрубку легко себе представить, если вообразить, что вы сворачиваете в трубку один из молекулярных слоёв графита – графен (рис.1).

Способ сворачивания нанотрубок – угол между направлением оси нанотрубки по отношению к осям симметрии графена (угол закручивания) – во многом определяет её свойства. Конечно, никто не изготовляет нанотрубки, сворачивая их из графитового листа. Нанотрубки образуются сами, например, на поверхности угольных электродов при дуговом разряде между ними. При разряде атомы углероды испаряются с поверхности и, соединяясь между собой, образуют нанотрубки самого различного вида – однослойные, многослойные и с разными углами закручивания. В зависимости от угла закручивания нанотрубки могут обладать высокой, как у металлов, проводимостью, а могут иметь свойства полупроводников. Дальше речь пойдёт только о нанотрубках с высокой проводимостью.

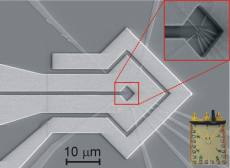
Открытия квантовой проводимости было впервые сделано у углеродных нанотрубок, когда измеряли зависимость их сопротивления от длины, погружая их в ртуть (см. рис. 2). Диаметр нанотрубок составлял от 1,4 до 50 нм, а длина – от 1 до 5 мкм. Но, несмотря на такой большой разброс в размерах сопротивление ВСЕХ нанотрубок составляло около 12,9 кОм.

Почему электричество в наномире превращается в оптику?

Ток переносится в проводнике электронами, образующими внутри него так называемый электронный газ. Среднеквадратичный импульс p одного из таких электронов можно найти из следующего соотношения для среднеквадратичной энергии E частицы идеального газа:

E=p²/(2m_e) = 3kT/2 , (2)

где k – постоянная Больцмана (1,38×10^-23 Дж/К), m_e – масса электрона (9,1×10^-31 кг). Подставляя в (2) Т=300 К, получаем p = 10,6×10^-26 кг×м/с.

Известно, что каждую частицу можно представить себе в виде волны де Бройля с длиной волны λ = h/p. Для электрона проводимости в металле получаем λ = 6,2 нм. Это значит, что для углеродных нанотрубок диаметром несколько нанометров или меньше электрон проводимости будет проявлять, главным образом, волновые свойства. Через такие нанотрубки электроны будут проходить, как световые волны проходят через световоды. Таким образом, электричество в наномире превращается в оптику, а джоулево тепло рассеивается только на границах наномира, где нанотрубка, например, соединяется с проводником обычных размеров.

Чему равен квант сопротивления R₀?

Попробуем вывести «на пальцах» красивейшую формулу (1), связывающую квант сопротивления с фундаментальными физическими константами. Так как нанотрубка обладает баллистической проводимостью, и джоулево тепло в ней не выделяется, можно считать, что её длина меньше длины свободного пробега электрона проводимости. Пусть между сечениями А и В нанотрубки приложено напряжение U, а сила тока в ней равна I (рис. 3).

Так как энергия не рассевается, то изменение энергии ΔЕ электрона между сечениями А и В составляет ΔЕ = eU. Это изменение энергии электрона произошло с ним за интервал времени Δt, равный времени пролёта между сечениями А и В. Соотношение неопределённостей Гейзенберга накладывает определённые ограничения на изменения ΔЕ и Δt :

ΔЕ · Δt ≈ h ,

откуда следует, что

U ≈ h/(e· Δt) . (3)

Оценим теперь силу тока в нанотрубке. Нанотрубка - одномерная квантовая структура. В ней, как в атоме гелия могут уживаться только два электрона, обладающие разными значениями спина. Это означает, что ток I между сечениями А и В нанотрубки равен:

I = 2e/Δt . (4)

Из соотношений (3) и (4) легко найти формулу для сопротивления R₀ нанотрубки между сечениями А и В :

R₀ = U/I = h/2e² ,

которая, как и следовало ожижать совпала с формулой (1).

Так как нагрев у нанотрубок отсутствует, они способны пропускать токи огромной плотности - более 10⁷ А/см². Если бы у углеродных нанотрубок была обычная (не баллистическая) проводимость, то при токах аналогичной плотности их температура выросла бы до 20 000 К, что гораздо выше температуры их сгорания (700 К).

Существование баллистической проводимости даёт зелёный свет инженерам, старающимся ещё и ещё уменьшить размеры электронных микросхем. Уменьшайте элементы микросхем до наноразмеров, и схемы перестанут нагреваться!

Информацию о других "загадочных" явлениях наномира можно найти в научно-популярной лекции «Что могут нанотехнологии», а ссылки на другие публикации - на личной страничке автора.

Реальные измерения электрических свойст - см. материалы раздела "Галерея".