Исследование структуры, электрических и оптических свойств полупроводниковых нанонитей активно проводятся последние несколько лет в связи с тем, что такие нанонити предоставляют много возможностей для новых наноразмерных электронных и оптоэлектронных устройств, таких как пьезоэлектрические наногенераторы [1], полевые транзисторы [2], светоизлучающие диоды [3,4], лазеры [5, 6] и волноводы [5-9]. Все эти применения возможны благодаря высокой кристалличности, низкой концентрации дефектов, гладким боковым границам и четко-выраженным торцам нанонитей, что делает их подходящими материалами для изготовления волноводов и резонаторов оптических мод в видимом и ближнем ИК диапазоне. В частности, широко исследуются нанонити из ZnO со структурой вюрцита - полупроводника с большой шириной запрещенной зоны, поскольку оксид цинка - многообещающий материал для производства наноразмерных светоизлучателей в ближнем УФ диапазоне [10-12]. К тому же ZnO простой в обращении, не токсичный материал, обладающий большой энергией связи экситона (60 мэВ) [9], что приводит к эффективному экситонному испусканию света даже при комнатной температуре. Нанонити ZnO могут быть выращены в больших количествах с определенным распределением по диаметрам и длиной до нескольких десятков микрометров. Рост нанонитей производят при высокой температуре по механизму "пар-жидкость-кристалл" (ПЖК), иногда в качестве катализатора используют золото.
Для введения света в полупроводниковые нанонити нами использованы нанонити из кварца [13]. Кварцевые нанонити и утонченные волокна в последние годы привлекают немало внимания, поскольку они могут быть легко получены оттягиванием на конус обычного кварцевого оптоволокна длиной несколько десятков миллиметров. Лазерный луч может быть легко введен извне в кварцевую нанонить через макроскопическое оптоволокно, к которому она остается прикрепленной.
В данной статье мы сообщаем, что комбинация кварцевых нанонитей, полученных в подходе «сверху вниз», и нанонитей ZnO, выращенных «снизу вверх», позволяет провести детальные экспериментальные исследования пассивных волноводных свойств полупроводниковых нанонитей. Конечно-разностные расчеты с учетом времени (FDTD) показали нам, что возможно достичь высокой эффективности стыковки оттянутых кварцевых волокон и нанонитей ZnO. Мы изучили затухающее поле в нанонитях ZnO как функцию их диаметра и проанализировали условия для одномодового и многомодового светопереноса. И в экспериментах и в расчетах мы обнаружили, что для нанонитей ZnO характерным диаметром около 250 нм и лазерного излучения видимого диапазона стыковка нанонитей ZnO и SiO2 часто приводи к возбуждению волновых мод высоких порядков. Мы также использовали нашу комбинацию кварцевых волокон и нанонитей ZnO для изучения испускания световых мод низкого порядка торцами нанонитей ZnO и сравнили результаты с нашими расчетами.
Синтез монокристаллических нанонитей оксида цинка проводили в горизонтальной трубчатой печи по газотранспортной методике [14]. Прекурсор (высокочистый порошок ZnO) помещали в корундовую лодочку и нагревали до 1620K, при этом происходило его испарение. Кремниевую подложку, покрытую 4 нм пленкой золота, помещали в холодный конец трубчатой печи при температуре около 1370K. Пар к подложке (где происходил катализируемый рост нанонитей ZnO по ПЖК механизму [15]) транспортировался при давлении 100 мбар газовым потоком аргона (50 мл/мин). По данным сканирующей электронной микроскопией (SEM) нанонити непосредственно после получения имели характерную длину до 100 мкм и диаметр от 40 до 500 нм, что определено. Рентгеноспектральным микроанализом обнаружены только сигналы цинка и кислорода в соотношении, отвечающем стехиометрии; просвечивающей электронной микроскопией и рентгеновской дифракцией подтверждено, что нанонити имеют структуру вюрцита, и ось c совпадает с продольной осью нанонити.
Полученные нанонити ZnO длиной 20-80 мкм рассеяли по поверхности тонкой стеклянной подложки, покрытой 80 нм пленкой мезопористого оксида кремния [16, 17]. Мезопористые пленки с монодисперсными порами диаметром 8 нм наносили методом dip-coating. Полученные пленки имели показатель преломления около n = 1.185 для видимого спектрального диапазона [16], препятствуя паразитной стыковке волноводов с подложкой. Совокупность с экстремально высокой гомогенности и гладкости этих слоев позволяет минимизировать потери на внешних границах кварцевых нанонитей и нанонитей ZnO, что является ключевым моментом при исследовании стыковок и волноводных процессов. Поскольку показатели преломления мезопористого оксида кремния значительно ниже, чем у нанонитей ZnO и SiO2, при численном моделировании мы можем считать нанонити свободными волноводами, окруженными воздухом.
Кварцевые нанонити с малыми световыми потерями были изготовлены традиционным методом вытягивания волокон [18] для получения нитей субмикронного диаметра, которые одним концом остаются прикрепленными к стандартному волокну. Установка для вытягивания волокон состояла из регулируемой водородной горелки и двух управляемых компьютером линейных платформ. Параметры для системы вытягивания волокон (скорость, ускорение, напряжение волокна и положение пламени) оптимизировались для достижения низких световых потерь в конусообразных частях волокон.
Для изучения стыковки и световодных свойств нанонитей ZnO мы запускали постоянное лазерное излучение (l = 532 нм, P = 1 мВ) в кварцевое волокно, расположенное на микропозиционной платформе. Мы использовали, как только полученные, так и разрезанные вблизи конической части кварцевые нанонити для введения света в нанонити ZnO. Стыковку волноводов мы наблюдали в инвертированный микроскоп с погруженным в масло 100х объективом (числовая апертура 1.4); прецизионное подведение конца кварцевого волокна к отдельным нанонитям ZnO осуществляли с помощью микропозиционной платформы.
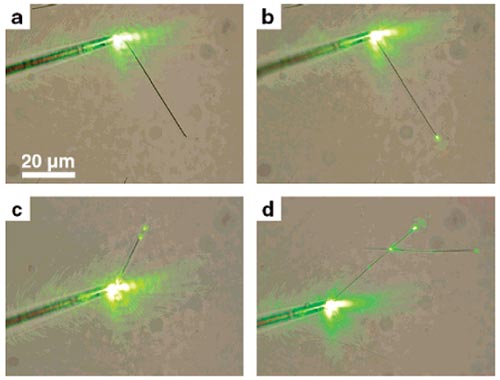
На рисунке 1 показан переход зеленого лазерного луча из оттянутого кварцевого волокна в нанонить ZnO. Мы наблюдаем полное отсутствие связи между двумя волноводами (рисунок 1а) до тех пор, пока расстояние между ними не станет меньше 1 мкм, тогда свет появляется на торце нанонити (рисунок 1b). На рисунке 1c показано испускание света на несовершенствах роста вдоль нанонити. Из рисунка 1d видно, что свет также эффективно переходит между двумя нанонитями ZnO, которые лежат одна на другой.
Для понимания значимости свойств и механизмов, управляющих стыковкой волноводов и процессами распространения света, изображенных на рисунке 1, мы провели численные моделирования распределения оптических мод видимого диапазона, в котором оксид цинка является полностью прозрачным. Мы начали с аналитически разрешимой модели, приближая нанонити ZnO идеальным цилиндром, пренебрегая их гексагональной структурой. Моделирования включали учет рассеяние в ZnO в приближении уравнения Сэлмейера [19]. На рисунке 2 показана зависимость доля энергии мод низкого порядка HE11, которые распространяются внутри цилиндрических нанонитей ZnO. Крестами отмечены переходы между одномодовым и многомодовым режимами, полученные из условия для одиночной волновой моды [20]: 2pd/l0(n12- nair2)1/2 < 2.405, где d - диаметр волокна, l0- длина волны в вакууме, n1 и nair - показатели преломления оксида цинка и воздуха соответственно. Переход происходит, когда доля энергии проводимой оксидом цинка составляет менее 80%. Критический диаметр для одиночной волновой моды d лежит в диапазоне от 350 нм (l = 800 нм) до 150 нм (l = 400 нм). Из рисунка 2 видно, что доля энергии проводимой внутри нанонити резко падает ниже критического диаметра, особенно при коротких длинах волн. Результаты рисунка 2 согласуются с предыдущими результатами, полученными для кварцевых и кремниевых нанонитей [20]. Поскольку диаметр нанонитей ZnO составляет приблизительно 250 нм, при длинах волн ниже 600 нм мы можем ожидать возбуждения волновых мод высоких порядков.
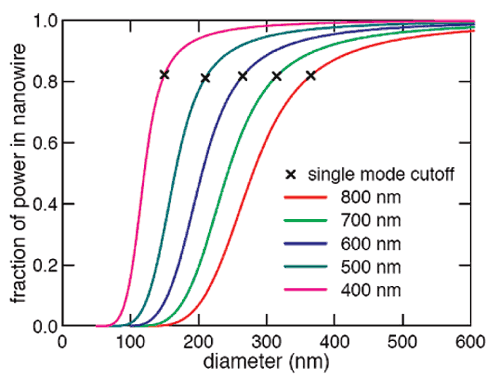
Рисунок 2. Зависимость доли энергии, переносимой модами низких порядков от диаметра нанонити и длины световой волны.
На рисунках 3a и 3b видно, что небольшие изменения во взаимной ориентации кварцевых конусных волокон и нанонитей ZnO значительным образом изменяет условия соединения волноводов и переноса света. На рисунке 3a соединение, перенос и испускание световых мод аналогично рисунку 1b, но небольшая коррекция конусного волокна ведет к возбуждению световых мод высоких порядков (рисунок 3b). Эти моды высоких порядков несут значительную долю дополнительной энергии по поверхности нанонитей и даже снаружи нанонитей в виде затухающее поле. Это можно увидеть, сравнив интенсивности свечения концов нанонитей на рисунках 3a и 3b.
Моды высоких порядков могут также возбуждаться на несовершенствах вдоль нанонитей ZnO. На рисунке 3c показан переход из одномодового в мультимодовый режим. На микрофотографиях нановолокон (рисунок 3d) видно, что диаметр в точке перехода увеличивается.
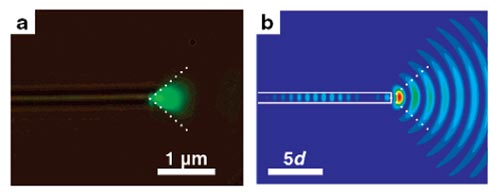
На рисунке 4a показано увеличенное изображение конца нанонити, изображенной на рисунке 3a, и профиль испускаемой световой волны. Белыми пунктирными линиями отмечен угол эмиссии близкий к 90º. На рисунке 4b показаны результаты двумерных конечно-разностных расчетов [21] испускания одномодового импульса нанонитью ZnO с (показателя преломления взят равным 2). Мы изобразили квадрат напряженности
электрического поля в направлении оси z (перпендикулярно плоскости рисунка) после того, как импульс был испущен правым концом нанонити. Небольшая часть света отражается и движется обратно к левому краю нанонити. Линейные размеры даны в единицах диаметра нанонити ZnO (dZnO), а длина волны выбрана равной 2.66dZnO, что соответствует ситуации на рисунке 4a (l = 532 нм, d = 200 нм). Моделирования подтверждают наши экспериментальные наблюдения испускания световой волны нанонитью в конус с углом близким к 90º, как показано белыми пунктирными линиями на рисунке 4a.
Наши результаты на рисунках 2 и 3 демонстрируют, что нанонити с диаметром около 200 нм могут служить как мольтимодовые волноводы для видимого света. Для определения максимально достижимой эффективности соединения световодов и понимания происхождения и свойств световодных мод высоких порядков, мы численно моделировали соединение и перенос света между кварцевыми и ZnO нанонитями используя FDTD методику [21]. Результаты FDTD моделирования масштабируемы если длина волны и линейные размеры нанонитей умножаются на одно число, в то время как показатели преломления исследуемых материалов остаются постоянными. Для расчетов приведенных здесь мы использовали следующие показатели преломления nZnO = 2, nSiO2 = 1.46, nair = 1, что является хорошим приближением для длин волн 400-1000 нм. Во всех расчетах вектор напряженности электрического поля перпендикулярен плоскости нанонити. Мы моделировали распространение импульса света из кварцевых волокон в нанонити ZnO в двух направлениях при различных углах между осями симметрии двух нанонитей как показано на врезке рисунка 5a. Импульс света однородно освещает левый конец кварцевого волокна, возбуждая моды низкого порядка, которые движутся вправо. На стыке между кварцевыми и ZnO нанонитями часть импульса отражается, часть рассеивается, а часть переходит в волноводные моды в нанонитях ZnO.
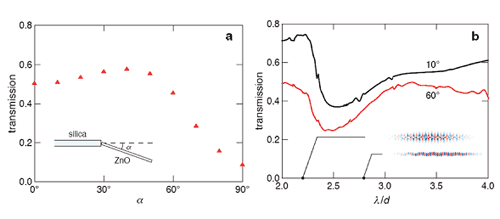
Для оценки эффективности перехода мы рассчитали пропускание в нанонитях ZnO делением полной энергии в нанонитях ZnO на полную энергию перешедшую в кварцевые нанонити. Рисунок 5a показывает как это пропускание зависит от угла между нанонитями для нанонитей диаметром dSiO2 = 4dZnO и длинной волны импульса (измеренной в вакууме) в три раза большей диаметра нанонитей ZnO, так что l = 200 нм, dZnO = 200 нм, dSiO2 = 800 нм, в соответствии с экспериментальными условиями. Расчеты показывают, что эффективность перехода превышает 50% для углов до 50º. Выше 50º пропускание существенно уменьшается, оставаясь выше 0.1 даже когда нанонити перпендикулярны друг другу. Варьирование длины волны в диапазоне 2dZnO - 4dZnO (здесь не приводиться) изменяет пропускание менее чем на 0.1. Более того, мы обнаружили, что пропускание слабо зависит (<0.1) от отношения диаметров в диапазоне 2 < dSiO2 / 4dZnO < 4. Введение небольшого зазора между двумя нанонитями (ширина зазора £ l/5) уменьшает пропускание всего лишь на несколько процентов.
Рисунок 5b показывает зависимость пропускания от длины волны для двух углов между нанонитями (10º и 60º). Масштабные длины волн лежат в диапазоне 2dZnO - 4dZnO, что для наших экспериментальных условий (dZnO = 200 нм) соответствует 400 нм < l < 800 нм. Для обоих углов спектры пропускания имеют общий. Главное различие между спектрами для двух углов заключается в том, что пропускание при 60º примерно на 0.10-0.25 меньше. Это различие вполне согласуется результатами, представленными на рисунке 5a. Спектры пропускания показывают, что эффективность переноса уменьшается с уменьшением длины волны от значения 4dZnO; расчеты показывают, что это уменьшение связано увеличением рассеяния на стыке между нанонитями. При длинах волн ниже 2.5dZnO пропускание резко возрастает для обоих углов. При угле в 10º пропускание превышает 0.7, что значительно выше, чем при больших длинах волн.
На врезке рисунка 5b показаны профили мод пропускаемого импульса при длинах волн от 2.2dZnO до 2.8dZnO. Голубой и красный цвета соответствуют максимумам отрицательной и положительной напряженности электрического поля. Профиль для длинноволнового импульса показывает моду низкого порядка, что проявляется в зигзагообразном распространении сквозь нанонити ZnO. Профиль для коротковолнового импульса показывает дополнительные составляющие мод высокого порядка с большой напряженностью электрического поля на поверхности нанонити и значительными напряженностями затухающего поля.
Волноводные свойства полупроводниковых нанонитей до сих пор практически не исследованы, хотя их фотолюминесценция экспериментально изучалась [10, 11, 22, 23]. Одной из причин является отсутствие надежной, эффективной и хорошо понимаемой оптической техники для изучения отдельных нанонитей. На рисунке 1 показано, что оттянутые кварцевые волокна и кварцевые нанонити являются удобными, надежными и эффективными инструментам для введения света в волноводном режиме в одиночные полупроводниковые нанонити. Рисунки 1a и 1b показывают, что таким образом в нанонити ZnO может быть введено значительное количество света. Наша методика позволяет проводить необходымиые систематические исследования волноводных свойств полупроводниковых нанонитей. Эти приемы могут быть также использованы для проверки нанонитей на наличие возможных несовершенств и источников дополнительных потерь (как показано на рисунке 1c) перед их дальнейшим использованием в устройствах. Эта простая система из двух нанонитей на рисунке 1d показывает, что оттянутые кварцевые волокна могут быть использованы для характеристики качества и потерь в более сложных оптических устройств на нанонитях.
Подложка из мезопористого оксида кремния с низким показателем преломления и низкими световыми потерями исключает паразитное рассеяние, не мешая исследованию волоноводных характеристик. Поскольку свет не испускается и не рассеивается никакой частью кроме торцов нанонитей (рисунок 1b), мы можем заключить, что в нанонитях ZnO нет значительных потерь в ходе светопереноса модами низкого порядка. Большие различия в показателях преломления материалов волноводов и мезопористым кварцем позволяет нам напрямую сравнивать результаты эксперимента с расчетами для "волновода в воздушной среде".
Показатели преломления полупроводниковых нанонитей обычно лежат в интервале 2-4 и длина волны в этих материалах lair/n значительно уменьшается. Следовательно критический диаметр для одномодового светопереноса заметно меньше, чем для кварцевых нанонитей. И наоборот, для нанонитей фиксированного диаметра предел перехода из одномодового в мультимодовый режим светопереноса сдвинут в голубую часть спектра по сравнению с кварцевыми нанонитями. На рисунке 2 показано, что в критической для одномодового режима точке 80% энергии переносится в небольшой пространственной области диаметром 150-350 нм, что точно совпадает с диапазоном диаметров нанонитей ZnO, выращиваемых по ПЖК механизму. Сильное ограничение весьма желательно для эффективного светопереноса на наноуровне с низкими потерями.
Большие различия в показателях преломления между ZnO и кварцевыми нанонитями приводит к возбуждению в нанонитях ZnO мод высоких порядков со значительным вкладом затухающего поля даже для нанонитей с диаметром лишь немного превышающим одномодовый предел. Эти затухающие поля рассеиваются на поверхности нанонитей, в то время как моды высокого порядка распространяются вдоль волоновода, приводя к появлению зеленого свечения на рисунке 3b. Моды высокого порядка, показанные на рисунке 3b, распространяются по волноводу без внутренних потерь и, следовательно, резко отличаются от мод "галереи шепота", о которых ранее сообщалось в нано- и микростержнях ZnO [24].
Как экспериментальные результаты (рисунки 3a, b) так и расчеты (рисунок 5b) показывают, что возбуждение мод высокого порядка контролируется оринетацией нанонитей. В зависимости от применения могут быть предпочтительны моды либо низкого либо высокого порядка. Например, сильная пространственная ограниченность, наблюдающаяся для мод низкого порядка, приводит к низким световым потерям в волноводе. Подобным образом моды низкого порядка могут максимизировать взаимодействие световой волны с полупроводниковым материалом в полупроводниковых усилителях. С другой стороны, моды высоких порядков могут быть использованы для увеличения эффективности стыковки, как показано на рисунках 3a и 3b.
Наши эксперименты показывают, что волны могут быть запущены в нанонити ZnO под большими углами. В соответствии с принципом обратимости хода лучей, углы запускания и углы испускания должны быть одинаковыми. Действительно, конус испускания нанонитей имеет угол близкий к 90º, как показано на рисунке 4. Пока этот угол велик, испускание остается прямолинейным и конец нанонити не может рассматриваться как точечный источник света, как ранее сообщалось для интенсивно светящих коротких нанонитей ZnO [25].
FDTD моделирования, представленные на рисунке 5 подтверждают высокую эффективность стыковки волноводов из кварцевых волокон и нанонитей ZnO. Хотя экспериментально достижимая эффективность может быть значительно ниже теоретического значения 0.5, расчеты показывают, что эффективность мало чувствительна к точной ориентации волноводов до углов 50º. Этот максимальный угол в 50º хорошо согласуется с экспериментальным наблюдением конуса испускания с углом 90º. С экспериментальной точностью половина угла этого конуса соответствует углу, при котором эффективность стыковки, по данным расчетов, начинает падать. Моделирования показывают, что главным физическим параметром, определяющем эффективность соединения, является большая разность показателей преломления волноводных материалов. Все эти результаты качественно не изменяются при повороте плоскости поляризации из состояния перпендикулярного плоскости волновода в плоскость волновода. Хотя абсолютные значения пропускания для двух поляризаций отличаются, возбуждение мод высоких порядков при малых длинах вол наблюдается для обоих типов поляризации.
На рисунке 5b показано, что для длин волн выше 2.5dZnO пропускание возрастает с ростом длины волны. Профиль электрического поля, полученный из расчетов, показывает, что с ростом длины волны рассеяние на стыке между двумя волноводами уменьшается, увеличивая долю света, перешедшего в нанонить ZnO. Для всех исследованных углов пропускание достигает минимума при длине волны около 2.5dZnO. Ниже этой длины волны пропускание значительно возрастает. Как видно из профилей на вставке рисунка 5b это возрастание происходит одновременно с возбуждением мод высокого порядка при переходе световой волны из кварцевого волокна в нанонить ZnO.
Таким образом, мы использовали кварцевые нанонити и оттянутые на конус кварцевые волокна для эффективного и контролируемого введения лазерного луча в отдельные нанонити ZnO и исследования их волноводных характеристик. Нанонити ZnO помещались на стеклянную подложку, покрытую мезопористым оксидом кремния с низким показателем преломления, для предотвращения перехода части света из кварцевых волокон в стеклянную подложку и обеспечения очень низкого паразитного рассеяния света на внешних границах нанонитей. Конечно-разностные расчеты показали зависимость эффективности стыковки нанонитей из SiO2 и ZnO от угла между ними и длины волны переносимой световой моды. Максимально достижимая теоретическая эффективность составляет 50%. Мы показали, что светоперенос мод высоких порядков с высокими интенсивностями на поверхности нанонитей часто наблюдается, когда свет переносится между нанонитями с различными показателями преломления. Мы изучили условия одномодового и мультимодового светопереноса для нанонитей ZnO численным моделированием и рассчитали силу затухающего поля моды низшего порядка в цилиндрической нанонити ZnO. Мы проанализировали испускание световых волн из нанонити ZnO и обнаружили, как в расчетах, так и в эксперименте, что типичный угол испускания для нанонитей диаметром 200 нм составляет 90º. Зависимость от длины волны величины пропускания и состояния мод высокого порядка представленные здесь позволяют интерпретировать опыты с полупроводниковыми нанонитями и оптимизировать устройства на их основе.
Список литературы
- Wang, Z. L.; Song, J. Science 2006, 312, 242.
- Li, Y.; Qian, F.; Xiang, J.; Lieber, C. M. Mater. Today 2006, 9, 18.
- Huang, Y.; Duan, X.; Lieber, C. M. Small 2005, 1, 142.
- Bao, J.; Zimmler, M. A.; Capasso, F. Nanoletters 2006, 6, 1719.
- Pauzauskie, P. J.; Yang, P. Mater. Today 2006, 9, 36.
- Hauschild, R.; Kalt, H. Appl. Phys. Lett. 2006, 89, 123107.
- Law, M.; Sirbuly, D. J.; Johnson, J. C.; Goldberger, J.; Saykally, R.J.; Yang, P. Science 2004, 305, 1269.
- Ye, Z.; Hu, X.; Li, M.; Ho, K.-M.; Yang, P. Appl. Phys. Lett. 2006, 89, 241108.
- Maslov, A. V.; Ning, C. Z. Appl. Phys. Lett. 2003, 83, 1237.
- Look, D. C. Mater. Sci. Eng.2001, B80, 383.
- Voss, T.; Bekeny, C.; Wischmeier, L.; Gafsi, H.; Bo¨rner, S.; Schade, W.; Mofor, A. C.; Bakin, A.; Waag, A. Appl. Phys. Lett. 2006, 89, 182107.
- Wischmeier, L.; Voss, T.; Bo¨rner, S.; Schade, W. Appl. Phys. A 2006, 84, 111.
- Tong, L.; Gattass, R. R.; Ashcom, J. B.; He, S.; Lou, J.; Shen, M.; Maxwell, I.; Mazur, E. Nature 2003, 426, 816.
- Borchers, C.; Mu¨ller, S.; Stichtenoth, D.; Schwen, D.; Ronning, C. J. Phys. Chem. B 2006, 110, 1656.
- Wagner, R. S.; Ellis, W. C. Appl. Phys. Lett. 1964, 4, 89.
- Konjhodzic, D.; Bretinger, H.; Wilczok, U.; Dreier, A.; Ladenburger, A.; Schmidt, M.; Eich, M.; Marlow, F. Appl. Phys. A 2005, 81, 425.
- Schmidt, M.; Boettger, G.; Eich, M.; Morgenroth, W.; Huebner, U.; Meyer, H. G.; Konjhodzic, D.; Bretinger, H.; Marlow, F. Appl. Phys. Lett. 2004, 85, 16.
- Gattass, R.; Svacha, G.; Tong, L.; Mazur, E. Opt. Exp. 2006, 14, 9408.
- Yoshikawa, H.; Adachi, S. Jpn. J. Appl. Phys. 1997, 36, 6237.
- Tong, L.; Lou, J.; Mazur, E. Opt. Exp. 2004, 12, 1025.
- Farjadpour, A.; Roundy, D.; Rodriguez, A.; Ibanescu, M.; Bermel, P.; Joannopoulos, J. D.; Johnson, S. G.; Burr, G. Opt. Lett. 2006, 31, 2972.
- Zhao, Q. X.; Willander, M.; Morjan, R. E.; Hu, Q.-H.; Campbell, E. E. B. Appl. Phys. Lett. 2003, 83, 165.
- Yi, G.-C.; Wang, C.; Park, W. I. Semicond. Sci. Technol. 2005, 20, S22.
- Nobis, T.; Kaidashev, E.; Rahm, A.; Lorenz, M.; Grundmann, M. Phys. ReV. Lett. 2004, 93, 103903.
- Vugt, L. K.; van Ru¨hle, S.; Vanmaekelbergh, D. Nanoletters 2006, 6, 2707.
Перевод: Дмитрия Цымбаренко



 Авторы - молодцы!
Авторы - молодцы!
