Нанотехнологическое сообщество Нанометр, все о нанотехнологиях
на первую страницу Новости Публикации Библиотека Галерея Сообщество Объявления Олимпиада ABC О проекте
 
  регистрация
помощь
 
Рис. 1. Размерные зависимости свойств различных веществ.
r - размер кристаллита, l - толщина пленки, d - толщина образца:
а - параметр кристаллической решетки для кремния [11] ( кривая 1) и двуокиси церия [12] (кривая 2); б - критическая температура сверхпроводимости и производная критического магнитного поля для пленок олова на стекле [16]; в - термоэдс пленочной термопары медь-константан как функция толщины пленки меди при постоянной толщине пленки константана [18]; г - зависимость прочности на разрыв (схематически) от толщины кристалла [19, 20]
Рис. 2. Размерные зависимости свойств высокотемпературного сверхпроводника ЕuВа2Сu3Оу от толщины пленки [21]:
б - удельное сопротивление и отношение сопротивлений при 300 К и 100 К
Рис. 2. Размерные зависимости свойств высокотемпературного сверхпроводника ЕuВа2Сu3Оу от толщины пленки [21]:
а - критическая температура сверхпроводимости Тс и параметр кристаллической решетки С0
Рис. 3. Размерные зависимости фазовых превращений:
а - содержание гексагональной фазы в аэрозольных частицах йодистого
серебра [22]; б - переход "аморфная фаза — кристаллическая фаза" в пленках различ¬ных веществ как функция толщины пленки [23 - 25]; в - зависимость времени кристаллизации аморфной сурьмы от толщины пленки [25]
Рис. 4. К обоснованию понятия "элементарная единица кристалла":
а - обобщенная размерная функция кристалла [10],
6 - общий вид зависимости "молекулярного" свойства от массы образца, состоящего из молекул,
в - зависимость свободной энергии кристаллической частицы от количества атомов (молекул) в ней - термодинамическое условие стабильности элементарной единицы кристалла

О вторичной структуре кристаллов

Ключевые слова:  вторичная структура кристаллов, мнение, периодика

Автор(ы): Веснин Юрий Иванович

Опубликовал(а):  Веснин Юрий Иванович

13 ноября 2007

Продолжение авторской статьи о вторичной структуре кристаллов

Вторичная структура кристаллов — исторический аспект

Проблема вторичной структуры твердого тела вновь возникла в самом начале современного этапа развития кристаллографии. После создания теории дифракции рентгеновских лучей в кристаллах стало очевидно, что основной, первичной структурой является атомная струк­тура кристалла. Однако Дарвин [1] обратил внимание, что эксперимен­тально наблюдаемые интенсивности дифракции можно согласовать с теорией лишь приняв, что кристаллы состоят из микрообластей — блоков размером около 10-4 см. Расчеты Дарвина были подтверждены, и наличие блочной структуры кристаллов — надежно установленный факт. В настоящее время принято считать, что реальные кристаллы со­стоят из блоков размером 10-4 - 10-5 см.

На существование вторичной структуры указывали и другие факты, например, наблюдения за ростом кристаллов (многочисленные данные на этот счет приведены в обзорах [2, 3, 4]). В начале 30-х годов ХХ столетия Цвикки сделал попытку обосновать расчетным путем вторичную структуру кристаллов, взяв за основу силы поверхностного натяжения [5]. Однако эти расчеты оказались неверными [6]. Попытки обосновать вторичную структуру кристалла в дальнейшем предпринимались неоднократно. Наиболее известные из них: "Кооперативные явления в кристаллах" А. Гётца (1935 г.) [2], "Мицеллярная теория металлов" Ю.А. Клячко (1933-35 г.г.) [3]. На этой основе в 30-х годах возникла обширная дискуссия, в которой приняли участие многие известные ученые (Борн, Смекаль, Брэгг, Фридель и другие). Эта дискуссия имела большое значение для развития науки о кристаллах, так как дала толчок созданию современной теории реальной структуры кристалла. Основа этой теории — понятие о структурном дефекте (точечном, линейном и др. [7]).

Идеи о вторичной структуре кристалла, высказанные в 30-х годах нашего столетия, по существу возрождали на новой основе воззрения более раннего ("доатомистического") периода развития кристаллографии. В XIX столетии значительное распространение имела теория структуры кристаллов, созданная Р.-Ж. Гаюи. Согласно этой теории, кристалл состоит из мельчайших параллелепипедов, названных "интегрирующими" и "сустрактивными" молекулами [8]. Близкие по духу идеи выдвигал Е.С. Федоров, считавший, что "всякий кристалл состоит из параллелоэдров (многогранников). Каждый параллелоэдр рассматривается как некая кристаллическая молекула" [9].

Размерная зависимость свойств кристаллов - экспериментальные данные

Современное развитие физики и химии твердого тела дало много новых фактов о реальной структуре и свойствах кристаллов. В частно­сти, были получены многочисленные данные о "размерном эффекте" — зависимости свойств кристаллических твердых тел при последователь­ном уменьшении их размеров. Такие данные были систематизированы и обобщены в работе [10]. На этой основе было сформулировано поня­тие "элементарная единица кристаллического твердого тела" ("квант кристалла"), обоснована необходимость этого понятия для единого и непротиворечивого объяснения известных экспериментальных данных. Впоследствии были сформулированы также некоторые определения, теоремы и следствия, развивающие представления о вторичной структуре кристаллов [33].

В настоящее время количество экспериментальных данных о размерном эффекте в кристаллах значительно возросло, повысились их качество и достоверность. Используя эти современные данные, рассмотрим на конкретных примерах, как изменяются свойства разных веществ при уменьшении размера кристалла.

На рис. 1а показана зависимость параметра решетки от величины кристаллита для кремния [11] и двуокиси церия [12] . Видно, что отклонения от параметра массивного образца происходят в интервале 10-5 - 10-6 см. Существенно, что эти данные получены рентгеновским методом, так как электронографические данные часто противоречивы ввиду меньшей точности и возможности неконтролируемого нагрева образца [13].

Аналогичные по виду зависимости известны для олова [14], окиси магния [15] и некоторых других веществ. На рис. 1б показаны зависимости критической температуры сверхпроводящего перехода и производной критического магнитного поля от размера кристаллита в пленках олова [18]. Отклонения от значений массивного образца начинаются в интервале размеров 10-5 – 10-6 см. Зависимости, показанные на рис. 1б, достаточно типичны для сверхпроводников, находящихся в мелкодисперсном состоянии [17].

Размерная зависимость термоэдс пленочной термопары медь-константан [18] отклоняется от значений массивного образца также вблизи 10-5 см (рис. 1в).

На рис. 1г схематически представлена размерная зависимость прочности на разрыв различных кристаллических образцов — нитевидные кристаллы ("усы") металлов и солей, тонкие плоские монокристаллы ("щепки") щелочных галогенидов. поликристаллические пленки металлов, проволочные образцы [19, 20]. Возрастание прочности относительно "массивных" значений начинается здесь вблизи 10-4 см. то есть при больших значениях толщины образцов. Вероятная причина этого - низкая величина "массивной" прочности материалов, что может быть связано со случайными факторами (наличие трещин, дефектов и пр.).

Интересно сопоставить размерные зависимости нескольких свойств одного и того же образца. На рис. 2 приведены данные, по­лученные в работе [21] для пленок высокотемпературного сверхпро­водника ЕuВаСu3Оу. Видно, что размерные зависимости различных свойств имеют идентичный характер. Величина свойства быстро изменяется от своего "массивного" значения при толщине пленки 10-5 – 10-6 см.

Эффектные примеры размерных зависимостей дает изучение структурных превращений мелкодисперсных образцов. На рис. 3а пока­зано, как изменяется кристаллическая структура аэрозольных частиц йодистого серебра при уменьшении размера частицы. При размере свыше 7x10-6 см почти все частицы имеют кубическую структуру. Вблизи размера 5х10-6 см происходит фазовое превращение и все частицы меньшего размера имеют структуру гексагональной модификации иодида серебра [22]. Интересно, что, согласно [22], аэрозольные частицы кубического иодида серебра состоят из отдельных блоков размером около 3.6x10-6 см при размере самих частиц более 7х 10-6 см.

Близкие по характеру размерные зависимости структурных превращений известны для тонких пленок различных веществ [23]. Для тонкопленочных образцов, наряду с превращениями кристаллических модификаций данного вещества, часто наблюдается фазовое превращение "аморфная фаза - кристаллическая фаза". Размерная зависимость этого превращения неоднократно изучалась для разных веществ. При комнатной температуре в области малых толщин часто реализуется аморфная фаза. Когда в процессе напыления достигается определенная критическая толщина пленки, происходит самопроизвольная кристаллизация. Критическая толщина обычно находится в интервале 10-5 – 10-6 см (рис. 3б). Такие данные известны для пленок сурьмы, висмута, теллурида германия, иттербия и других веществ [23, 24]. Для пленок сурьмы детально изучена кинетика превращения и показано, что при комнатной температуре время перехода стремится к нулю, когда толщина пленки возрастает от 2,5x10-6 см до 1x10-5 (см. рис. 3в). При толщине пленки менее 2,5x10-6 см аморфная фаза стабильна, то есть скорость превращения бесконечно мала (пунктир на рис. 3в) [25].

Размерная функция кристалла и понятие "элементарная единица твердого тела"

Число примеров размерных зависимостей, подобных рассмотренным выше, может быть значительно увеличено. Необходимо отметить характерные особенности рассмотренного экспериментального материала:

1. Разнообразие свойств. Можно предположить, что аналогичные зависимости будут наблюдаться для любого свойства, которое зависит от кристаллической структуры вещества.

2. Разнообразие веществ. Представлены вещества различных классов, общим для них являются: а) кристаллическое состояние; б) достаточно малый размер кристаллита.

3. Размерные зависимости во всех рассмотренных случаях выглядят практически аналогично. При уменьшении раз­мера образца величина свойства вначале не изменяется или изменяется незначительно. Существенные изменения свойств начинаются при размере кристаллита 10-5 – 10-6 см.

4. Совершенно очевидно, что наблюдаемое единообразие размерных зависимостей должно иметь одну причину, общую для всех веществ и свойств. Принято считать, что изменение свойств мелкодисперсных образцов можно объяснить увеличением удельной поверхности, возрастанием доли атомов, находящихся на поверхности частиц. Экспериментальные данные рис. 1-3 позволяют сделать вывод, что увеличение удельной поверхности не может быть причиной наблюдаемых изменений различных свойств кристаллов в интервале 10-5 – 10-6 см. Это очевидно, например, для электрических свойств, в том числе сверхпроводящих, для прочности (как показано в [26]) и некоторых других свойств. По-видимому, невозможно объяснить поверхностными эффектами изменения структуры частиц и пленок, аналогичные показанным на рис. 3. Совершенно очевидно также, что изменения параметра решетки кристаллов в интервале 10-5 – 10-6 см, аналогичные показанным на рис. 1а, не могут быть вызваны какими-либо причинами, связанными с поверхностью. В этом случае изменения параметра могли бы произойти лишь в нескольких поверхностных атомных слоях. Эксперимент показывает, что изменения параметра решетки имеют объемный характер (десятки и сотни атомных слоев, то есть весь объем частицы). Поэтому такие изменения обычно связывают не с поверхностью, а с другими причинами, например, с "внутренним давлением" [12].

5. Очевидно также, что различные структурные дефекты не могут вызвать наблюдаемые изменения разных свойств вблизи критического размера.

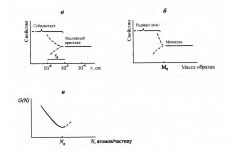
На основании п.п. 1-3 можно сформулировать понятие размерной функции кристалла, общее для любых кристаллов и их свойств (r-функция кристалла). Обобщенная r-функция кристалла имеет вид, показанный на рис. 4а. При уменьшении размера кристалла величина свойства остается практически постоянной вплоть до критического размера rq=10-5 – 10-6 см, изменяясь затем в ту или иную сторону (пунктир на рис. 4а).

Ранее отмечалось [10], что вид, аналогичный рис. 4а, имеет размерная функция для образца, состоящего из молекул (атомов), если измеряется какое-либо внутримолекулярное (атомное) свойство (рис. 4б). Величина свойства изменится, когда размер (масса) образца станет меньше размеров (массы) отдельной молекулы (атома). Эта аналогия позволяет ввести понятие "элементарная единица кристалла" [10].

Элементарная единица кристаллического твердого тела ("квант кристалла" или "минимальный кристалл" - "мик") определяется следующим образом. Минимальный кристалл - мик - есть такое минимальное количество кристаллического твердого тела, которое еще сохраняет нормальные ("предельные") свойства, характерные для массивного образца данного вещества. Кристалл меньшего размера утрачивает (существенно изменяет) эти свойства. Размеры мика для различных веществ лежат в пределах 10-5 – 10-6 см. Некоторые экспериментальные данные [11, 12, 22, 28] дают основание полагать, что наиболее вероятное значение rq =(3 - 4) х 10-6 см. При таком размере мик содержит 106 - 108 атомов (молекул), его форма и симметрия должны определяться характером и симметрией межатомных (межмолекулярных) взаимодействий.

Размерная функция кристалла (рис. 4а) является необходимым условием для введения понятия "элементарная единица кристалла": если эта единица реально существует, размерная функция должна иметь вид, показанный на рис. 4а. Условие достаточности этого понятия — отсутствие каких-либо других причин, объясняющих наблюдаемый вид r-функции в общем случае, с учетом разнообразия свойств. Следовательно, вводимое понятие "элементарная единица кристалла" удовлетворяет обоим формальным логическим критериям истинности понятия. На основе данного понятия в принципе можно объяснить размерную зависимость любого свойства для любого кристаллического вещества, хотя механиз­мы реализации таких зависимостей для разных свойств могут быть различны. При этом определяющим фактором является размер кристаллита. Для пленок и нитевидных образцов критическим размером должна быть толщина, равная размеру элементарной единицы (мика). Сравнительно плавные изменения свойств вблизи критического размера вполне объяснимы полидисперсностью образцов.

Некоторые следствия, связанные с понятием "элементарная единица кристалла"

Обязательным термодинамическим условием стабильности элементарной единицы кристалла является наличие минимума свободной энергии вблизи размера rq. Это эквивалентно наличию минимума свободной энергии для некоторого числа Nq структурных единиц (атомов или молекул), содержащихся в кристаллической частице (рис. 4в). Наличие минимума означает повышенную устойчивость частиц такого размера (например, при механическом воздействии на кристалл). Этот вывод согласуется с известными экспериментальными фактами о существовании предела измельчения кристаллов при механическом воздействии, в частности, при механохимической обработке [27] или предельной механической деформации [28].

Минимум свободной энергии (рис. 4в) эквивалентен наличию минимума на размерной зависимости потенциальной энергии взаимодействия атомов или молекул, составляющих кристалл. Потенциальная энергия может изменяться лишь за счет изменения межатомных расстояний в кристалле. Отсюда с необходимостью следует, что для малых частиц при r < rq (N < Nq) должно наблюдаться изменение межатомных расстояний - параметра кристаллической решетки (см. рис. 1а). Наличие минимума свободной энергии (рис. 4в) означает также, что при N < Nq кристаллические частицы должны иметь повышенную удельную энергию, вызванную дефицитом массы частиц. По-видимому, с этой энергией связаны известные свойства нанофазных частиц и материалов.

Таким образом, концепция элементарной единицы кристалла вполне согласуется с известными экспериментальными данными. Кроме того, эта концепция естественным образом решает проблему вторичной структуры кристаллов. Предполагается, что в нормальных (равновесных) условиях все кристаллы состоят из элементарных единиц - миков. Особый интерес представляет проблема границ между ними. Известные экспериментальные данные позволяют предположить, что границы между миками могут служить источником и местами развития дислокаций. По-видимому, не является случайным тот факт, что максимальная плотность дислокаций (1011 - 1012 на 1 см2) практически соответствует числу элементарных единиц на 1 см2 сечения кристалла при линейном размере мика 3х10-6 см. Некоторые экспериментальные данные [29, 30] дают основание полагать, что реально существующие границы между миками являются путями, по которым через кристалл осуществляется транспорт вещества (диффузия) и зарядов (электрический ток).

Концепция элементарной единицы твердого тела ("надмолекулы") успешно развивается в течение ряда лет в известных работах В.Б. Алесковского и его школы [31, 32]. Этими работами убедительно показана практическая значимость подходов, основанных на понятии "элементарная единица кристалла", показано, что современные пред­ставления о вторичной структуре кристаллов могут быть прочным фундаментом экспериментальной химии твердого тела.

СПИСОК ЛИТЕРАТУРЫ

  1. Darwin G., Phil. Mag. - 1914. - (6), 27. - P. 675 - 681.
  2. Göetz A., Int. Conf. Physics. - 1935. - 2. - P. 62-71.
  3. Клячко Ю.A., Усп. химии. - 1939. - 8, № 9. - С. 1314-1346.
  4. Иоффе B.C., Там же. - 1944. - 13, № 2. - С. 144-161.
  5. Zwicky F., Proc. Nat. Acad. Sci. USA. - 1929. - 15. - P. 253 - 258.
  6. Orowan E., Z. Phys. - 1932. - 79. - P. 573-579.
  7. Фридель Ж., Дислокации. - M.: Мир, 1967. - 643 с.
  8. Гаюи Р.-Ж., Опыт теории структуры кристаллов и ее применения к разнородным кристал­лическим веществам. - М.: АН СССР, 1962. - 450 с.
  9. Шубников А.В., У истоков кристаллографии. - М.: Наука, 1972.
  10. Веснин Ю.И., О зависимости свойств кристалла от его размера. Деп. ВИНИТИ, № 2123 - 70 Д. - Новосибирск, 1970. - 22 с.
  11. Hamasaki M., Adachi Т. et at., J. Appl. Phvs. - 1978. - 49. - P. 3987-3992.
  12. Гамарник М.Я., ФТТ. - 1988. - 30, № 5. - С. 1399-1404.
  13. Петров Ю.И., Кластеры и малые частицы. - М.: Наука, 1986. - С. 188.
  14. Vook R.W., Parker Т., Wright D., Surface-interface - chemical and physical characierislics / Ed. E. Burke, Syracuse. - N.Y., 1967. - P. 347.
  15. Cimino A., Porta P.. Valigi M., J. Am. Ceram. Soc. - 1966. - 49. - P. 152-156.
  16. Голянов В.М., Демидов А.П. и др., ЖЭТФ. - 1970 - 58, № 2. - С. 528-534.
  17. Веснин Ю.И., Ультрадисперсные частицы и их ансамбли. - Киев: Наук, думка, 1982. - С. 128-135.
  18. Chopra K.L, Bahl S.K., Randlett M.R., J. Appl. Phys. -1968. - 39, N 3. — P. 1525-1528.
  19. Бережкова Г.В., Нитевидные кристаллы. - М.: Наука. 1969. - С. 81.
  20. Гофман Р.У., Физика тонких пленок. — М.: Мир, 1968. — Т. 3. — С. 292.
  21. Michikami О., Asahi М., Asano Н., Jap. J. Appl. Phys. - 1990. - 29, N 2. - P. L298 - L301.
  22. Горбунов Б.З., Какуткина Н.А., Куценогий К.П., Мороз Э.М., Кристаллография. - 1979. - 24, № 2. - c. 334-337.
  23. Чопра К.Л., Электрические явления в тонких пленках. - М.: Мир, 1972. - 434 с.
  24. Лазарев Б.Г., Кузьменко В.М. и др., Физика металлов и металловед. 1971. - 32, № 1. — c. 52—57.
  25. Палатник Л.С., Косевич В.М., Докл. АН СССР. - 1958. - 121, № 1. - С. 97-101.
  26. Beams J.W., Structure and Properties of Thin Films / Ed. C. Neugebauer. - N.Y.. 1958. - P. 183.
  27. Аввакумов Е.Г., Механические методы активации химических процессов. - Новосибирск: Наука, 1986.
  28. Wood W.A., Rachinger W.A., Nature. - 1948. - 162. - P. 891-892.
  29. Косенко B.E., ФТТ. - 1961. - 3. № 7. - С. 2102-2105.
  30. Лазарев Б.Г., Овчаренко О.Н. и др., Bопр. атомн. науки и техн. Сер. фундамент. и прикл. сверхпровод. - 1974. - Вып. 1(2). - С. 23 - 24
  31. Алесковский В.Б., Стехиометрия и синтез твердых соединений – Л. Наука, 1976.
  32. Алесковский В.Б., Курс химии надмолекулярных соединений. - Л.; Изд ЛГУ, 1990.
  33. Веснин Ю.И., Вторичная структура кристаллов. - Новосибирск, 1994. - 31 с - (Препринт / РАН. Сиб. отд-ние, Институт неорганической химии; № 94-01).


В статье использованы материалы: Нанометр


Средний балл: 9.0 (голосов 3)

 


Комментарии
Ненашев Илья Николаевич, 13 ноября 2007 23:54 
это что ж получается, нормального кристалла размером полтора "мик"-а быть не может? или мик - всё же не квант? Но как тогда быть с привязкой размера мик-а к количеству неоднородностей на единицу объёма?
Зубцов Михаил Николаевич, 14 ноября 2007 22:36 
Глубокоуважаемая редакция!
А нельзя ли получить на email обе статьи в виде .pdf файла? На мой взгляд, это очень нужная, хотя - и спорная,- во всяком случае - для меня, - и актуальная работа. Кроме того, я посылал email по указанному в шапке статьи адресу, но ответа не получил. Может быть кто-то, кто близок к этой тематике может подсказать: есть ли англоязычные публикации автора по этой тематике? Мне в WoS ничего не удалось найти. Заранее благодарен за ответы.
С уважением
Да в принципе можно, конечно. Выберу время и сделаю. Посылать по адресу, который в регистрационной карточке?
Зубцов Михаил Николаевич, 19 ноября 2007 09:57 
Глубокоуважаемый Евгений Александрович! Прошу извинить, но - физически не мог ответить сразу. Да и сейчас еще не вполне работоспособен. Если возможно, перешлите статью на адрес указанный мною при регистрации на сайте.

Глубокоуважаемый(ая) Душа! Не так все просто. Дело не в теориях, а в том, что в твердом теле структуры на поверхности и под поверхностью не идентичны. А флуктуации в плотности распределения примесных ионов в кристаллической матрице полупроводника определяются, судя по всему, именно подповерхностными флуктационными искажениями кристаллической решетки матрицы.
В статье я не увидел явного бреда. По поводу отношения к таким публикациям - см. начало первой статьи того же автора. АРГУМЕНТИРОВАННО критиковать любые публикации - это Ваше право, милости просим. В споре рождается истина.
Зубцов Михаил Николаевич, 19 ноября 2007 11:06 
Глубокоуважаемый Евгений Алексеевич, к сожалению, умудрился переврать Ваше отчество - извините.
Уважаемая редакция! Я также очень бы хотел получить полную версию статей коллеги Веснина. По крайней мере там есть над чем поразмыслить, а новое всегда кажется странным. В чем-то, как я понял, эти работы перекликаются с работами профессора Майкова. Мне лично это весьма любопытно. Благодарю за внимание.
Dusha, 19 ноября 2007 23:54 
>АРГУМЕНТИРОВАННО критиковать
Как можно аргументировано критиковать то, в чем ничего нет, кроме новой терминологии?
Вы можете привести какой-нибудь контрольный тест, эксперимент, который бы позволил сказать: старые представления неверны, новые это предсказали?
Конечно в статье нет бреда, я такого не писал. Опус - это легкая беллетристика без особого смысла, это в статье есть.
>[B]в твердом теле структуры на поверхности
и под поверхностью не идентичны[/B]
И до этих статей не было теорий, которые эти явления количественно описывали? То есть все технология допирования полупроводников - чисто эмпирическая область? Извините, вот это чушь.
А товарищ не приводит ни одного примера расчета с помощью своей теории.
Много новых слов и никакого прогресса.
"Много новых слов и никакого прогресса" - без комментариев
Палии Наталия, 20 ноября 2007 13:38 
Конечно, данная статья весьма актуальна, хотя еще в 2001 г о "размерном эффекте" задумывался H. Gleiter (Gleiter H, Weissmuller J, Wollersheim O, et al.Nanocrystalline materials: A way to solids with tunable electronic structures and properties? ACTA MATERIALIA 49 (4): 737-745 FEB 23 2001 {Times Cited: 43}, текст этой статьи можно скачать из elibrary, если Ваша организация имеет подписку, а Вы сами зарегистрированы в ней). Появление этой публикации лишь говорит о том, что не все проблемы решены.
Еще одно замечание - в стандарте ASTM Е-2456-06 "Terminology of Nanotechnology" (его тоже можно скачать за $ 0, т.е. бесплатно, с сайта ASTM) определены как "transitive", так и "non-transitive" nanoparticles, таким образом оговаривается, что не для всяких веществ уменьшение размера частиц приводит к резкому изменению свойств. - Так что суть явления еще до конца не познана, и появление новых публикаций заставляет еще и еще раз задумываться о подобных явлениях. javascript:insertsmile(' ', 'editor');
Уважаемый Евгений Алексеевич,

сообщите, пожалуйста, Зубцову Михаилу Николаевичу мой электронный адрес: yu_vesnin@ngs.ru, так как мой рабочий
e-mail мне пока недоступен.

Ю.И. Веснин
Dusha, 20 ноября 2007 16:39 
>хотя еще в 2001 г о "размерном эффекте" задумывался H. Gleiter
Да размерный эффект известен еще от царя Гороха! Активность половины промышленных катализаторов определяется размером активного компонента, ширина запрещенной зоны полупроводников зависит от размера, .... и этим данным не 5 лет.
Другое дело, что спекулируя этими размерными зависимостями, автор пытается вводить новые сущности, причем совершенно безосновательно, бездоказательно и более того, совершенно не рассматривая факты, которые напрямую противоречат его идеям.
К примеру, основным положением статьи является тезис о существовании "квантов" кристаллов с универсальным размером 10-100нм и неупорядоченных границ между ними. Возьмите монокристалл чего-нибудь, сделайте микроскопический образец и попробуйте эти границы найти
Я согласен с тезисом о том, что не все размерные эффекты объяснены в настоящее время, но сказав: "квант" - вы не прибавили ничего к пониманию этих явлений.
Найти "мозаичную структуру" или оценить "области когерентного рассеяния" можно, но называть их "квантами"...
Dusha, 22 ноября 2007 14:16 
>"области когерентного рассеяния"
Одной из причин появления такого рода "теорий" как раз и является нежелание (или неспособность) авторов задумываться над физическим смыслом общепринятых терминов, они просто берут терминологию, вкладывают в нее некое свое понимание (большей частью весьма поверхностное) и развивают на этой основе некие представления не имеющие отношения к действительности.
ОКР - очень хороший пример такого (кстати, весьма распространенного) непонимания, даже среди рентгенщиков. Почему-то ОКР представляются как некие идеально регулярные области с четко обозначенными границами между ними (узнаете кристаллические кванты? ). Но если вдуматься и вспомнить, что ОКР определяется как величина обратная ширине дифракционного пика, то становится понятно, что никаких границ там нет (точнее, они не обязательно должны быть), а ОКР - это просто область на которой искажения решетки достигают полпериода, что меняет конструктивную интерференцию рентгеновской волны на деструктивную. И где теперь кванты искать?
Зубцов Михаил Николаевич, 22 ноября 2007 15:04 
Глубокоуважаемый(ая) Dusha! Если я правильно понял Ваши замечания, то Вам известна работа или работы в которых представлена микроскопическая теория локальных немонотонных искажений кристаллографической структуры твердых растворов (отклонения от стехиометрии, возникновение локальных или протяженных областей аморфизации, возникновение некристаллографических пентагональных включений, итп.) дающая аналитические выражения для связи параметров кристалла и составлящих кристалл атомов с размерами и геометрией такого рода локализованных флуктуационых отклонений от кристаллографического порядка. Не могли бы Вы дать ссылочку на эту статью (статьи). Заранее спасибо.
Dusha, 22 ноября 2007 18:12 
Уважаемый Михаил Николаевич!
Честно говоря, я слегка не разобрался в этом сложноподчиненном вопросе
Во-первых, я вообще ничего не говорил про немонотонность и теории. Единственно, что Вас могло навести на такую мысль, это достаточно очевидный тезис о том, что огромная микроэлектронная индустрия не могла бы работать, если бы процессы диффузии под поверхностью полупроводников(читай: допирование) не были бы описаны с высокой точностью и достоверностью. Но это не значит, что я перечитывал весь этот ворох работ.
Во-вторых, речь про твердые растворы тоже не шла. Речь шла про размерные эффекты вообще в кристаллах.
Если Вы имеете ввиду общую универсальную теорию, описывающую все свойства многокомпонентных нестехиометрических систем в зависимости от любых микро-искажений, то очевидно, что такой нет быть и не может.
Работы же, описывающие конкретные проявления локальных неоднородностей, имеются, надо просто сделать библиотечный запрос. Например, по влиянию концентрации точечных дефектов на скорости диффузии допантов: поиск по "defect enhanced diffusion" вернул около 100 000 ссылок.
Мы тоже не так давно опубликовали статью, где экспериментально показали (электронной томографией), что диффузия идет преимущественно вдоль дислокаций и по градиенту напряжений.
Зубцов Михаил Николаевич, 22 ноября 2007 20:48 
Глубокоуважаемый(ая) Dusha! Не зная Вашего имени и отчества, право, я не знаю как к Вам обращаться. Обращаться по nicname я, честно говоря, не очень привык, потому вынужден прибегать к безличному Вы.

Насколько я понимаю со слов тех, кто пытается разрабатывать IC с размером элементов менее 65-50 нанометров, все они указывают на реально существующую проблему локальной пространственной неоднородности физических свойств подложки, причем, речь идет не столько о таких эффектах как локализация или грануляция плотности допанта, но об эффектах которые можно было бы истолковывать как некие локальные объемные изменения (то ли наведенные в процессе обработки подложки, то ли возникающие еще в процессе роста кристалла) кристаллической структуры, приводящие к локальным (на длинах нескольких десятков нанометров) изменениям, которые, в свою очередь, можно было бы трактовать как эффект локального изменения зонной структуры. То есть, это выглядит как наличие некоторой структуры кристаллически "правильных" доменов, - в которой каждый домен представляет собой "правильный" кристаллит, - разделенных аморфизированными областями. Кроме того, это можно было бы трактовать так, как если бы соседние кристаллиты или объемы имели разный состав и несовпадающую ориентацию кристаллографических осей. То есть, все это выглядит так, как если бы процессы диффузии протекали в некоторой квазиполикристаллической структуре, либо - в монокристалле, но с некоторой вторичной структурой обуславливающей последующее неоднородное распределение электронных и дырочных свойств, что, собственно, и регистрируется. Понятно, что все это лишь трактовка, возможно - ошибочная. Прямых измерений нет, да и непонятно, как и чем это можно было бы мерить. Вместе с тем, эффект явно присутстует. Поэтому я и обратился к Вам со своим вопросом: быть может Вам известны попытки построения микроскопической теории описывающей подобные локальные искажения кристаллографической структуры твердых растворов, поскольку, как я понимаю, упоминаемые Вами точность и достоверность описания как раз к этому случаю и не относятся. Что же касается работы Ю.И Веснина, то он как раз предлагает модельное описание именно такой ситуации. Чем его статья меня и прельстила. Если Вам известны иные модельные описания природы и свойств таких локальных неоднородностей (а лично мне кажется, что все они носят флуктуационный характер)- буду Вам весьма признателен за ссылки.
Dusha, 22 ноября 2007 21:41 
Хотел было предложить Вам перенести нашу дискуссию на форум, поскольку она явно вышла за рамки обсуждаемой статьи, но не обнаружил на форуме раздела для научных дискуссий
Евгений Алексеевич, мы можем как-нибудь исправить это упущение? А то как-то несолидно: назвались научным сайтом, а на форуме только азбука, политика и пурга.


Обращайтесь ко мне по нику, это нормально и не столь академично, как ИО. Я мужского рода, как явствует из окончаний глаголов прошедшего времени в предыдущем посте . Специализируюсь на просвечивающей электронной микроскопии, как явствует из фотографий в галерее.

>То есть, это выглядит как наличие некоторой структуры кристаллически "правильных" доменов, - в которой каждый домен представляет собой "правильный" кристаллит, - разделенных аморфизированными областями.
Нет этого в промышленных вафлях, смею Вас заверить. Я довольно много смотрю (в том числе на высоком разрешении, то есть вижу атомы) экспериментальные и промышленные образцы девайсов, подложка всегда - это монокристаллы с некоторой плотностью дислокаций, но дислокации (одномерные дефекты, а не двумерные границы) разделены не десятками нм, а десятками микрон.
И честно говоря, никогда в литературе и в обсуждениях не встречался с подобной проблемой. Может стоит посмотреть, что конкретно эти ребята делают?
Измерить можно, напрямую посмотрев в электронном микроскопе, мы можем регистрировать отклонения параметров кристаллов до 10-4, а уж аморфную фазу увидим в любом случае.
>[B]Вместе с тем, эффект явно присутстует.
....
модельные описания природы и свойств таких локальных неоднородностей (а лично мне кажется, что все они носят флуктуационный характер)[/B]
В чем эффект-то собственно заключается? Не его интерпретация, а исходные данные. На каких системах это наблюдается? О каких конкретно твердых растворах идет речь? Так в SiGe действительно при некоторых условиях наблюдается выпадение некоей загадочной фазы, и известно, что InP имеет свойство диффундировать при нагреве и образовывать точки. Известно, опять же, что примеси скапливаются в ядрах дислокаций.
Я не очень понимаю, как Вы можете говорить о теории того, что является не наблюдаемым фактом, а лишь одним их возможных предположений? Давайте факты и поищем теории, которые их могли бы объяснить...
>он как раз предлагает модельное описание именно такой ситуации
Да ничего он не предлагает. Он просто вводит новые термины для известных явлений. Причем заведомо некорректные.
Dusha, 23 ноября 2007 00:55 
Thanx!

> и отвлеченных науных тем.
Размещаю по просьбе автора статьи:

Ненашеву И.Н. Кристалл может быть любого размера. Если он размером в 1,5 мика, то это мик + субкристалл. Мик – аналог гигантской молекулы. Даже в простых молекулах могут быть такие варианты, например, О2 + О  О3 (озон).
Марголину В.И. Наиболее полно ВСК описана в монографии "Вторичная структура и свойства кристаллов". Изд. СО РАН, Новосибирск, 1997 г., 105 стр. Можно получить по адресу: www.sibran.ru .
Некоторые вопросы связаны с недостаточным знакомством с теорией ВСК. В первой статье рис. 1 показывает лишь упрощённую схему основной структуры ВСК. Промежутки между миками (1 атомный слой) всегда заполнены собственными атомами кристалла, либо атомами примесей. Этот слой повторяется примерно через 100 обычных слоёв. О степени порядка атомов в этом слое – пока неясно. В очень чистых кристаллах (например, Si) слой Т-пространства занят теми же атомами Si. Вряд ли его можно увидеть в микроскоп. Для этого нужно заполнить Т-слой другими атомами, т.е. образец готовится специально. Например, диффузионным способом, т.к. диффузия идёт по Т-пространству. Подробнее об этом в книжке.
Поскольку статьи прочитали многие (уже более 1,5 тыс. обращений), то некоторые вопросы будут сняты после знакомства с прилагаемой краткой аннотацией глав монографии.

КРАТКАЯ АННОТАЦИЯ ГЛАВ МОНОГРАФИИ

Глава 1

Отмечено, что проблема вторичной структуры кристаллов (ВСК) имеет долгую историю. Даётся краткий исторический обзор. Рассмотрены современные экспериментальные данные по размерной зависимости свойств кристаллов. Показано, что эти данные являются необходимым и достаточным условием для введения нового понятия: "Элементарная единица кристалла". Выводы и следствия на основе этого понятия согласуются с экспериментом.

Глава 2
На основе понятия "Элементарная единица кристалла" сформулированы основные положения теории вторичной структуры кристаллов, определения, теоремы, следствия. Вводятся новые понятия: мик, субкристалл, Т-пространство и др.

Глава 3
С позиций теории ВСК рассмотрены и обоснованы механизмы атомной диффузии в кристаллах (быстрая и медленная диффузия). Показано, что диффундирующие атомы образуют в Т-пространстве особый тип твёрдых растворов – твёрдые растворы размещения.

Глава 4
С позиции ВСК рассмотрены некоторые экспериментальные закономерности диффузии: влияние размера атома, анизотропия диффузии, корреляция между скоростью диффузии и предельной растворимостью примеси.

Глава 5
Анализируется соотношение между изоморфными и твёрдыми растворами размещения. Рассмотрен распад изоморфных твёрдых растворов с образованием зон Гинье-Престона в Т-пространстве кристалла. На примере твёрдых растворов алюминия показано, что выводы теории ВСК согласуются с экспериментом.

Глава 6
Анализируется изменение свойств кристалла при уменьшении размера мика. Показано, что при таком уменьшении образуется субкристалл – аналог молекулы-радикала. Как и любой радикал, субкристалл имеет повышенную удельную энергию (в расчёте на атом) и реакционную способность. С этим связаны особые свойства наночастиц и наноматериалов. Субкристалл является "активным центром" твёрдого тела.

Глава 7
Рассмотрены некоторые вопросы, связанные с движением свободных электронов в Т-пространстве кристалла (закон Ома, взаимодействие электронов с атомами примесей, отрицательное дифференциальное сопротивление). По-новому трактуется механизм эффекта Ганна. Получена формула, связывающая частоту осцилляций Ганна с потенциалом ионизации примесных атомов. На примере кристаллов GaAs с примесью Si показано, что формула адекватно описывает реальный эксперимент.

Для того чтобы оставить комментарий или оценить данную публикацию Вам необходимо войти на сайт под своим логином и паролем. Зарегистрироваться можно здесь

 
Проникающие шарики
Проникающие шарики

Наносистемы: физика, химия, математика (2024, Т. 15, № 1)
Опубликован новый номер журнала "Наносистемы: физика, химия, математика". Ознакомиться с его содержанием, а также скачать необходимые Вам статьи можно по адресу: http://nanojournal.ifmo.ru/articles/volume15/15-1
Там же можно скачать номер журнала целиком.

Наносистемы: физика, химия, математика (2023, Т. 14, № 5)
Опубликован новый номер журнала "Наносистемы: физика, химия, математика". Ознакомиться с его содержанием, а также скачать необходимые Вам статьи можно по адресу: http://nanojournal.ifmo.ru/articles/volume14/14-5
Там же можно скачать номер журнала целиком.

Наносистемы: физика, химия, математика (2023, Т. 14, № 4)
Опубликован новый номер журнала "Наносистемы: физика, химия, математика". Ознакомиться с его содержанием, а также скачать необходимые Вам статьи можно по адресу: http://nanojournal.ifmo.ru/articles/volume14/14-4
Там же можно скачать номер журнала целиком.

Материалы к защитам магистерских квалификационных работ на ФНМ МГУ в 2023 году
коллектив авторов
30 мая - 01 июня пройдут защиты магистерских квалификационных работ выпускниками Факультета наук о материалах МГУ имени М.В.Ломоносова.

Материалы к защитам выпускных квалификационных работ бакалавров ФНМ МГУ 2022
Коллектив авторов
Материалы к защитам выпускных квалификационных работ бакалавров ФНМ МГУ 2022 содержат следующую информацию:
• Подготовка бакалавров на факультете наук о материалах МГУ
• Состав Государственной Экзаменационной Комиссии
• Расписание защит выпускных квалификационных работ бакалавров
• Аннотации квалификационных работ бакалавров

Эра технопредпринимательства

В эпоху коронавируса и борьбы с ним в существенной степени меняется парадигма выполнения творческих работ и ведения бизнеса, в той или иной мере касаясь привлечения новых типов дистанционного взаимодействия, использования виртуальной реальности и элементов искусственного интеллекта, продвинутого сетевого маркетинга, использования современных информационных технологий и инновационных подходов. В этих условиях важным является, насколько само общество готово к использованию этих новых технологий и как оно их воспринимает. Данной проблеме и посвящен этот небольшой опрос, мы будет рады, если Вы уделите ему пару минут и ответите на наши вопросы.

Технопредпринимательство в эпоху COVID-19

Небольшой опрос о том, как изменились подходы современного предпринимательства в контексте новых и возникающих форм ведения бизнеса, онлайн образования, дистанционных форм взаимодействия и коворкинга в эпоху пандемии COVID - 19.

Технонано

Технопредпринимательство - идея, которая принесет свои плоды при бережном культивировании и взращивании. И наша наноолимпиада, и Наноград от Школьной Лиги РОСНАНО, и проект Стемфорд, и другие замечательные инициативы - важные шаги на пути реализации этой и других идей, связанных с развитием новых высоких технологий в нашей стране и привлечением молодых талантов в эту вполне стратегическую область. Ниже приведен небольшой опрос, который позволит и нам, и вам понять, а что все же значит этот модный термин, и какова его суть.



 
Сайт создан в 2006 году совместными усилиями группы сотрудников и выпускников ФНМ МГУ.
Сайт модернизирован для ресурсной поддержки проектной деятельности учащихся в рамках ГК 16.647.12.2059 (МОН РФ)
Частичное или полное копирование материалов сайта возможно. Но прежде чем это делать ознакомьтесь с инструкцией.