Редакторы Нанометра придерживаются консервативных классических теорий строения и образования кристаллов и не являются сторонниками гипотез, обсуждаемых в приводимой ниже статье. Тем не менее, выносим по просьбе автора статьи на обсуждение Нанотехнологическим сообществом его гипотезу об альтернативной теории строения кристаллического состояния.
ВВЕДЕНИЕ
В настоящее время накоплен обширный массив опытных фактов, анализ которых неизбежно приводит к следующему выводу: атомно-молекулярная структура, оставаясь основой структуры кристалла, должна быть продолжена и дополнена еще одной ступенью организации кристаллической материи - вторичной структурой кристалла (ВСК). Ее следует рассматривать как основу вторичной структуры конденсированной материи, включая аморфное твердое тело и жидкость. Основу концепции вторичной структуры кристаллов составляет понятие "элементарная единица - квант кристалла" (Веснин, 1970). Это понятие в известной степени аналогично понятию "молекула" в химии. Элементарная единица кристалла рассматривается как индивидуальное образование - своего рода гигантская молекула твердого тела. На основе этого понятия построена последовательная теория вторичной структуры кристалла [1, 2], которая имеет целый ряд приложений в различных областях химии и физики твердого тела. Области приложений теории ВСК постоянно расширяются.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ВСК
Монокристалл состоит из элементарных единиц - миков (мик — минимальный кристалл). Для неорганических кристаллов типичный размер мика rМ 300 , он содержит nМ 106 - 108 атомов (молекул). Форма мика в кристалле — полиэдр, симметрия и форма которого определяются характером межатомных взаимодействий. Мики объединяются в группы (блоки), которые при слиянии образуют монокристалл. Промежутки между миками образуют в монокристалле единую связанную систему - Т-пространство кристалла, которое характеризуется пониженной электронной плотностью и измененными межатомными расстояниями. Элементы Т-пространства показаны на рис. 1 (кубический кристалл): 2-мерный элемент — дол, 1-мерный - лан, узел Т-пространства — ям. Основной параметр Т-пространства (расстояние между смежными гранями миков) - промежуток размером в один атомный слой (2-5 для большинства неорганических кристаллов). В эксперименте определяется как межплоскостное расстояние для наиболее интенсивного дифракционного отражения.
В Т-пространстве постоянно находятся атомы примесей, собственные атомы кристалла, а также свободные электроны. Эти атомы образуют особый тип твердых растворов — твердые растворы размещения с максимальной атомной (молекулярной) долей 2 - 3 %. Теория выделяет три основных типа твердых растворов размещения в зависимости от позиции атома в Т-пространстве кристалла. Свойства таких твердых растворов хорошо согласуются с известными экспериментальными данными [2].
Основное термодинамическое условие стабильности элементарной единицы кристалла - минимум на зависимости свободной энергии кристаллической частицы от числа составляющих ее структурных единиц (атомов, молекул) n при п = nM (рис. 2). Дополнительные минимумы G могут появляться при объединении миков в блоки. При п < nM кристаллическая частица является субкристаллом. Он имеет повышенную удельную энергию (энергия, приходящаяся на одну частицу) за счет дефицита массы относительно массы мика и связанного с этим возрастания взаимной потенциальной энергии структурных единиц. Поэтому субкристалл является центром сил притяжения для атомов и молекул окружающей среды, т. е. центром неспецифической адсорбции ("активным центром"). Этот вывод имеет принципиальное значение для химии твердого тела и материаловедения, так как создание "активных центров" - основной способ управления реакционной способностью твердого тела. Большое количество субкристаллов - "активных центров" - причина высокой энергонасыщенности нанофазных материалов и их особых свойств. Субкристаллы на поверхности твердого тела определяют его адсорбционные и каталитические свойства.
СУБКРИСТАЛЛ КАК АКТИВНЫЙ ЦЕНТР ГЕТЕРОГЕННОГО КАТАЛИЗА
Благодаря возрастанию взаимной потенциальной энергии U своих атомов (молекул), субкристалл является для окружающей среды центром дополнительных центростремительных сил F, так как dU/dx = F, где х - расстояние от кристалла. За счет этого он притягивает и удерживает молекулы окружающей среды (газ), образуя вокруг себя "активную сферу". В ней создается повышенное локальное давление (концентрация) окружающей газовой среды. Под действием силового поля субкристалла молекулы газа дополнительно поляризуются, изменяя свою геометрию и энергетические характеристики связей (модификация). Модифицированные молекулы реагируют между собой в объеме "активной сферы", образуя продукты реакции (гетерогенный катализ). Таким образом, при гетерогенном катализе взаимодействие происходит между молекулами, модифицированными в силовом поле "активной сферы" субкристалла при повышенном локальном давлении (концентрации) компонентов окружающей среды [2].
Анализ известного экспериментального материала [3, 4] показывает, что данная модель "активного центра" вполне адекватно отражает различные аспекты гетерогенного катализа, в том числе:
—процессы активирования катализатора;
—высокие скорости каталитических реакций;
—потерю активности при нагреве катализатора вне реакционной смеси выше температуры Таммана (субкристаллы, сливаясь, превращаются в элементарные единицы - мики);
—повышение удельной активности при размере кристаллита r < rМ (увеличивается объем "активной сферы");
—процессы ингибирования, отравления катализатора и др.
Количественное описание этих процессов возможно по мере развития аппарата теории ВСК применительно к модели "активного центра".
АНОМАЛИИ КОЭФФИЦИЕНТА РАСПРЕДЕЛЕНИЯ И СВОЙСТВ КРИСТАЛЛОВ В ОБЛАСТИ МАЛЫХ КОНЦЕНТРАЦИЙ ИЗОМОРФНОЙ ПРИМЕСИ
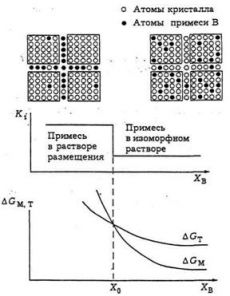
Аномалии коэффициента распределения K при росте кристалла из расплава (скачкообразное увеличение K при малой концентрации Хв изоморфной примеси - K-скачок) имеют важное значение для процессов кристаллизации и очистки веществ. Такие аномалии обнаружены для многих бинарных систем при атомной (молекулярной) доле Хв < 2-3 % [5, 6]. Для объяснения этого явления выдвинуто около 10 различных гипотез и предположений, однако общепринятой модели не существует. С другой стороны, в ряде работ [7, 8] были найдены аномалии различных свойств полупроводниковых твердых растворов в той же области концентраций (Хв < 2 %).
Аномалии различных свойств твердых растворов при малых концентрациях изоморфной примеси — одно из следствий теории ВСК [9]. Как отмечено выше, в промежутках между элементарными единицами – миками (Т- пространство монокристалла) постоянно находятся атомы примесей, а также собственные атомы кристалла. Эти атомы образуют особый класс твердых растворов — твердые растворы размещения с максимальной атомной (молярной) долей 2-3 %. В процессе роста кристалла из расплава при концентрации примеси Хв = Х0 < 2-3 % может произойти смена механизма вхождения примеси в кристалл. При Хв > Х0 примесь находится преимущественно в объеме миков в виде изоморфного твердого раствора. При Хв < Х0, ввиду уменьшения энтропийного фактора и роста свободной энергии G, атомам примеси энергетически более выгодно разместиться в промежутках между миками (Т-пространство), образуя твердый раствор размещения. Переход произойдет вблизи точки пересечения концентрационных кривых энергии смешения Гиббса DGсм = DHсм - ТDSсм (рис. 3). Необходимое условие такого перехода — достаточно большое положительное значение DHсм изоморфного раствора. В противном случае кривая DGM лежит слишком низко и пересечения с кривой DGT не будет. Положительное значение DHсм изоморфных растворов приобретает за счет деформационной энергии решетки, которая пропорциональна DR — разности атомных радиусов компонентов. Поэтому K-скачок наблюдается лишь при достаточно большом DR [6]. Теория ВСК объясняет все особенности этого явления: 1) возникновение K-скачка как следствие смены механизма вхождения примеси в кристалл; 2) согласно [2], концентрационная область K -скачка — область существования твердых растворов размещения (не более 2-3 % примеси); 3) увеличение, а не уменьшение концентрации примеси в кристалле при Хв < Х0; 4) необходимость достаточно большой разницы атомных радиусов изоморфных компонентов DR.
Смена механизма вхождения примеси в кристалл и типа твердого раствора может быть причиной вышеупомянутых аномалий свойств кристаллов вблизи Хв = Х0. Теория ВСК позволяет оценить характер таких аномалий. Систематическое изучение концентрационных зависимостей K и свойств кристаллов на одних и тех же образцах может иметь важное практическое значение для процессов роста и кристаллизационной очистки веществ. Особый интерес представляет более сложный случай - распределение примеси при кристаллизации водных растворов (влияние растворителя).
РАСПАД ИЗОМОРФНЫХ ТВЕРДЫХ РАСТВОРОВ (ЗОНЫ ГИНЬЕ-ПРЕСТОНА)
Наличие вторичной структуры кристаллов наглядно проявляется при распаде изоморфных твердых растворов. Пересыщенный твердый раствор распадается с образованием новой фазы. Рассмотрим этот процесс на примере кристалла с кубической формой мика (см. рис. 1). Атомы, концентрация которых избыточна для данных термодинамических условий, покидают объем мика и выходят в Т-пространство равномерно через все грани мика. Накапливаясь в близлежащих долах и ланах, эти атомы образуют агрегаты - зародыши новой фазы. В плоскости дола они должны иметь максимально симметричную форму, так как при максимальной симметрии достигается минимум взаимной потенциальной энергии атомов. Поэтому агрегаты имеют форму диска с максимальным диаметром rМ= 300 (ребро мика) и толщиной 2 - 5 (промежуток между гранями). Концентрация дисков равна числу миков в 1 см3 кристалла, умноженному на среднее число промежутков, т. е. СД 3×1016×3 1017/см3. Плоскости дисков ориентированы по главным кристаллографическим осям.
Другая часть атомов будет накапливаться в ланах, также образуя агрегаты. Располагаясь вдоль лана, они имеют форму иглы толщиной 3-8 . Ранее было показано. [2], что диффузия атомов вдоль лана идет с повышенной скоростью ("быстрая диффузия") и агрегаты-иглы легко сливаются в направлении диффузии. Поэтому их длина должна быть больше ребра мика (300 ), а концентрация — меньше числа ланов в 1 см3, т. е. СИ, < 1017/см3. Иглы также ориентированы по главным кристаллографическим осям. Форма и расположение агрегатов показаны на рис. 4.
В табл. 1 эти выводы сопоставлены с данными прямых электронно-микроскопических наблюдений кубических твердых растворов (сплавы на основе А1). Эти данные достаточно типичны и для других твердых растворов [10]. Видно, что выводы теории ВСК совпадают с экспериментом по всем параметрам: форма, размер, концентрация, кристаллографическая ориентация. В теории дисперсионного твердения материалов [10] диски названы зонами Гинье-Престона (ГП), иглы - зонами Гинье-Престона-Багаряцкого (ГПБ). Эти данные можно рассматривать как прямое экспериментальное подтверждение существования вторичной структуры кристаллов.
ТАБЛИЦА 1
Характеристики дисперсионных выделений при распаде твердых растворов на основе алюминия (данные[10])
|
Зона |
Форма |
Размеры, |
Количество в 1 см |
Пространственная ориентация |
Сплавы |
|
ГП, тип I |
Диск |
(20 - 200) ´ (3- 6) |
1016-1018 |
Главные кристалло- графические оси |
А1 - Ag, А1 - Си, Al - Zn, A1 - Zn - Mg |
|
ГПБ, тип II |
Игла |
((1-2)×103)´(3-10) |
3×1015 |
То же |
Al - Mg - Si |
ПОЛИМОРФНЫЕ ПРЕВРАЩЕНИЯ В КРИСТАЛЛАХ
Реакционная способность кристаллов в точке полиморфного превращения
Эффект значительного увеличения реакционной способности кристаллов в точке полиморфного превращения (эффект Хедвалла) давно известен и широко используется на практике [11]. Достаточно разработанного механизма этого явления не существует.
С позиций теории ВСК в процессе полиморфного превращения в кристалле (фаза 1 ® фаза 2) происходит разрушение изначальной вторичной структуры фазы 1. Если превращение происходит в области относительно невысоких температур (замедленная диффузия), вторичная структура фазы 2 формируется медленно. В этом случае вторичная структура должна состоять из субкристаллов фазы 2 (размер кристаллита менее 300 ). Согласно [2] (см. также рис. 2), такой кристалл имеет повышенную удельную энергию и высокую реакционную способность. Таким образом, с позиций теории ВСК механизм эффекта Хедвалла состоит в трансформации вторичной структуры в точке полиморфного превращения: мик фазы 1 ® субкристалл фазы 2.
Фазовыепревращения II рода и гибридный монокристалл
Известно, что при полиморфном фазовом переходе II рода в кристалле (фаза 1 ® фаза 2) вблизи точки перехода монокристалл состоит из микрообластей фаз 1 и 2 (гибридный монокристалл) [12, 13].
Согласно теории ВСК, дальний порядок в кристалле ограничен объемом мика [2]. Поэтому структурное превращение первоначально локализовано в этом объеме. При повышении температуры превращение распространяется в кристалле путем постепенного увеличения числа миков (или субкристаллов) фазы 2 за счет уменьшения числа миков фазы 1 (растянутое полиморфное превращение). Образуется гибридный монокристалл, в котором области фаз 1 и 2 сосуществуют [12]. При этом постепенно поглощается скрытая теплота превращения 1 ® 2. В эксперименте этот процесс проявляется в виде кажущегося увеличения теплоемкости. Когда превращение завершится, нормальный ход теплоемкости восстанавливается (l-точка).
ЗАКЛЮЧЕНИЕ
Вышеизложенное, а также другие приложения теории ВСК, рассмотренные ранее [2], позволяют сделать вывод, что данная модель вполне адекватно отражает различные процессы в твердом теле. С другой стороны, современная модель твердого тела построена целиком на уровне атомной структуры, в ней отсутствуют понятия вторичной структуры кристалла. Такая модель является неполной и не может вполне адекватно отражать действительность. Это можно было бы сравнить с попытками построить современные химические модели лишь на основе понятия "атом", игнорируя понятие "молекула". В современной химии и физике твердого тела это неизбежно приводит к многочисленным трудностям при описании свойств кристаллов, снижает способность теории прогнозировать реальный эксперимент, предсказывать новые факты и явления.
СПИСОК ЛИТЕРАТУРЫ
1. Ю. И. Веснин, Журн. структур, химии, 36 (1995) 724.
2. Ю. И. Веснин, Вторичная структура и свойства кристаллов, Изд-во СО РАН, Новосибирск, 1997.
3. Г. К. Боресков, Гетерогенный катализ, Наука, Москва, 1988.
4. Ж. Жермен, Гетерогенный катализ, Изд-во иностр. лит., Москва, 1961.
5. А. Н. Киргинцев, Л. И. Исаенко, В. А. Исаенко, Распределение примеси при направленной кристаллизации, Наука, Новосибирск, 1977.
6. Л. А. Нисельсон, А. Г. Ярошевский, Межфазовые коэффициенты распределения, Наука, Москва, 1992.
7. Б. Ф. Ормонт, Журн. физ. химии, 52 (1978) 342.
8. Я. А. Угай, Ю. М. Бондарев, Е. Г. Гончаров, А. М Ховив, Неорган, материалы, 23 (1987) 1945.
9. Yu. I. Vesnin, Abstracts European Crystallographic Meeting ECM-18, B3-P8, Praha, 1998.
10. А. Келли, Р. Никлсон, Дисперсионное твердение, Металлургия, Москва, 1966.
11. К. Мейер, Физико-химическая кристаллография. Металлургия, Москва, 1972.
12. А. Уббелоде, Плавление и кристаллическая структура, Мир, Москва, 1969.
13. A. J. Burggraaf, Ber. Bunsenges. Phys. Chem., 87 (1983) 208.
Адрес автора: 630090 Новосибирск, Весенний проезд, д.6, кв. 56, тел.(383)3308418; E-mail: yu_vesnin@ngs.ru
Монографию: Ю.И. Веснин "Вторичная структура и свойства кристаллов" можно приобрести в интернет-магазине по адресу: www-psb.ad-sbras.nsc.ru. Стоимость с пересылкой около 100 руб.